mirror of
https://github.com/Rucknium/misc-research.git
synced 2025-05-23 19:21:50 +00:00
First draft of Black Marble Flood: Best Options for Ring Size and Fee
This commit is contained in:
parent
5528aac9d9
commit
7823fc72c3
13 changed files with 4618 additions and 0 deletions
Monero-Black-Marble-Flood
|
|
@ -0,0 +1,99 @@
|
|||
|
||||
|
||||
|
||||
# Install gmp and ggplot2 packages:
|
||||
# install.packages(c("gmp", "ggplot2"))
|
||||
# May have to install this first: https://gmplib.org/
|
||||
|
||||
library(ggplot2)
|
||||
|
||||
|
||||
# Use equation 2.1 of
|
||||
# Holst, L. (1986). On Birthday, Collectors’, Occupancy and Other Classical Urn Problems.
|
||||
# International Statistical Review / Revue Internationale de Statistique, 54(1), 15–27. https://doi.org/10.2307/1403255
|
||||
|
||||
# "In this paper we will consider problems connected with drawing with replacement from
|
||||
# an urn with r balls of different colours."
|
||||
# "The inverse of the occupancy problem is sometimes called the coupon collector's
|
||||
# problem. It reads: how many draws are necessary for obtaining k different balls?"
|
||||
|
||||
# Our problem is a simplification where r = k. Then, r_(k) = r!
|
||||
|
||||
|
||||
total.nodes <- 1000L
|
||||
k <- 8L
|
||||
# k is number of distinct pruning slices
|
||||
|
||||
|
||||
coupon.pmf <- sapply(k:total.nodes, FUN = function(n) {
|
||||
r <- k
|
||||
gmp::div.bigq(
|
||||
gmp::mul.bigq(gmp::factorialZ(r), gmp::Stirling2(n = n - 1L, k = k - 1L)),
|
||||
gmp::pow.bigq(r, n)
|
||||
)
|
||||
}
|
||||
)
|
||||
|
||||
one.div.by.coupon.cdf <- vector("numeric", length(coupon.pmf))
|
||||
|
||||
for (i in seq_along(one.div.by.coupon.cdf)) {
|
||||
one.div.by.coupon.cdf[i] <- gmp::asNumeric(gmp::sub.bigq(1L, Reduce(gmp::add.bigz, coupon.pmf[1:i])))
|
||||
}
|
||||
|
||||
|
||||
|
||||
png("images/pruned-node-collectors-problem-to-100.png", width = 600, height = 600)
|
||||
|
||||
ggplot(data.frame(x = k:total.nodes, y = one.div.by.coupon.cdf), aes(x = x, y = y)) +
|
||||
geom_line() +
|
||||
labs(title = "Probability of not having all 8 distinct pruned\nslices on the Monero network (8-100 nodes)") +
|
||||
ylab("Probability (log scale)") +
|
||||
xlab("Nodes on network (log scale) github.com/Rucknium") +
|
||||
scale_x_log10(limits = c(8, 100), breaks = c(8, 16, 32, 64, 100)) +
|
||||
scale_y_log10(limits = c(1e-05, 1), breaks = 10^(0:-5)) +
|
||||
theme_set(theme_gray(base_size = 20))
|
||||
|
||||
dev.off()
|
||||
|
||||
|
||||
security.128.bit <- gmp::asNumeric(gmp::div.bigq(1L, gmp::pow.bigq(2L, 128L)))
|
||||
# https://bitcoin.stackexchange.com/questions/38512/is-12-word-seed-phrase-safe-enough
|
||||
|
||||
png("images/pruned-node-collectors-problem-to-1000.png", width = 600, height = 600)
|
||||
|
||||
ggplot(data.frame(x = k:total.nodes, y = one.div.by.coupon.cdf), aes(x = x, y = y)) +
|
||||
geom_line() +
|
||||
labs(title = "Probability of not having all 8 distinct pruned\nslices on the Monero network (8-1000 nodes)") +
|
||||
ylab("Probability (log scale)") +
|
||||
xlab("Nodes on network (log scale) github.com/Rucknium") +
|
||||
scale_x_log10(limits = c(8, 1000), breaks = c(10, 50, 100, 500, 1000)) +
|
||||
scale_y_log10(limits = c(1e-60, 1), breaks = 10^(c(0, -10, -20, -30, -40, -50, -60))) +
|
||||
theme_set(theme_gray(base_size = 20)) +
|
||||
geom_hline(yintercept = security.128.bit, linetype = 2) +
|
||||
annotate("text", x = 15, y = security.128.bit * 200, size = 6,
|
||||
label = "2^-128", parse = TRUE)
|
||||
|
||||
dev.off()
|
||||
|
||||
|
||||
n.nodes.lower.prob.than.128.bit.security.guessibility <-
|
||||
(k:total.nodes)[one.div.by.coupon.cdf <= security.128.bit][1]
|
||||
|
||||
print(n.nodes.lower.prob.than.128.bit.security.guessibility)
|
||||
|
||||
|
||||
# Probability of missing at least one of the pruning slices at least one
|
||||
# of the m times if all of the nodes re-draw the pruning seeds m times:
|
||||
|
||||
q <- 1000
|
||||
|
||||
# Use a network size of 100 nodes:
|
||||
|
||||
i <- which(k:total.nodes == 100)
|
||||
|
||||
1 - gmp::asNumeric(Reduce(gmp::add.bigz, coupon.pmf[1:i]))
|
||||
# Drawn once
|
||||
|
||||
1 - gmp::asNumeric(gmp::pow.bigq(Reduce(gmp::add.bigz, coupon.pmf[1:i]), q))
|
||||
# Re-drawn m times
|
||||
|
||||
690
Monero-Black-Marble-Flood/code/tradeoff-optimal-fee-ring-size.R
Normal file
690
Monero-Black-Marble-Flood/code/tradeoff-optimal-fee-ring-size.R
Normal file
|
|
@ -0,0 +1,690 @@
|
|||
|
||||
|
||||
# First, run tradeoff-output-index.R
|
||||
# Make sure to install the packages listed at the top there.
|
||||
|
||||
|
||||
|
||||
setwd("Monero-Black-Marble-Flood/pdf")
|
||||
# Set location of where images and tables should be saved
|
||||
|
||||
|
||||
|
||||
|
||||
num.blocks.before.spam <- uniqueN(output.index$block_height)
|
||||
|
||||
|
||||
|
||||
mean.non.spam.output.per.block <- nrow(output.index)/num.blocks.before.spam
|
||||
# 105
|
||||
|
||||
r <- mean.non.spam.output.per.block
|
||||
|
||||
non.spam.fingerprint.tx.sim <- copy(output.index[ ! duplicated(tx_hash) & tx_num != 1, ])
|
||||
# tx_num != 1 to remove coinbase outputs
|
||||
|
||||
|
||||
non.spam.fingerprint.tx.sim.tabulated.weight <- non.spam.fingerprint.tx.sim[, as.data.table(table(tx_weight_bytes, number_of_inputs))]
|
||||
non.spam.fingerprint.tx.sim.tabulated.weight <- non.spam.fingerprint.tx.sim.tabulated.weight[N != 0, ]
|
||||
non.spam.fingerprint.tx.sim.tabulated.weight[, tx_weight_bytes := as.numeric(tx_weight_bytes)]
|
||||
non.spam.fingerprint.tx.sim.tabulated.weight[, number_of_inputs := as.numeric(number_of_inputs)]
|
||||
non.spam.fingerprint.tx.sim.tabulated.weight[, N := as.numeric(N)]
|
||||
|
||||
|
||||
non.spam.fingerprint.tx.sim.tabulated.size <- non.spam.fingerprint.tx.sim[, as.data.table(table(tx_size_bytes, number_of_inputs))]
|
||||
non.spam.fingerprint.tx.sim.tabulated.size <- non.spam.fingerprint.tx.sim.tabulated.size[N != 0, ]
|
||||
non.spam.fingerprint.tx.sim.tabulated.size[, tx_size_bytes := as.numeric(tx_size_bytes)]
|
||||
non.spam.fingerprint.tx.sim.tabulated.size[, number_of_inputs := as.numeric(number_of_inputs)]
|
||||
non.spam.fingerprint.tx.sim.tabulated.size[, N := as.numeric(N)]
|
||||
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out <- non.spam.fingerprint.tx.sim[, as.data.table(table(number_of_inputs, number_of_outputs))]
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out <- non.spam.fingerprint.tx.sim.tabulated.in.out[N != 0, ]
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out[, number_of_inputs := as.numeric(number_of_inputs)]
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out[, number_of_outputs := as.numeric(number_of_outputs)]
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out[, N := as.numeric(N)]
|
||||
|
||||
|
||||
|
||||
|
||||
mean.coinbase.tx.size <- output.index[!duplicated(tx_hash) & tx_num == 1, mean(tx_size_bytes)]
|
||||
|
||||
|
||||
mean.size.1in.2out <- non.spam.fingerprint.tx.sim[number_of_inputs == 1 & number_of_outputs == 2, mean(tx_size_bytes)]
|
||||
mean.size.2in.2out <- non.spam.fingerprint.tx.sim[number_of_inputs == 2 & number_of_outputs == 2, mean(tx_size_bytes)]
|
||||
mean.size.16.ring.input <- mean.size.2in.2out - mean.size.1in.2out
|
||||
|
||||
mean.size.zero.ring.tx.size <- mean.size.1in.2out - mean.size.16.ring.input + 32 * 4
|
||||
# This "size zero ring" is so that the variable ring size can be added later
|
||||
# See below for why 32 * 4 is added
|
||||
|
||||
mean.size.16.ring.input <- mean.size.16.ring.input - 32 * 4
|
||||
# We subtract 32 bytes times 4 because
|
||||
# 1) The key image in the vin[[1]]$key$k_image JSON object is 32 bytes (64 characters
|
||||
# of hexcode, divided by two). There is one key image per ring.
|
||||
# 2-4) There are 3 other 32 byte strings in
|
||||
# rctsig_prunable$CLSAGs[[1]]$c1
|
||||
# rctsig_prunable$CLSAGs[[1]]$D
|
||||
# rctsig_prunable$pseudoOuts
|
||||
# that appear once per ring and do not seem to scale up with ring size.
|
||||
# The "mean.size.16.ring.input" will be one 32 byte string for the ring signature
|
||||
# string per each ring member, plus some amount (about 3) bytes for
|
||||
# the average storage space per integer output index in vin[[1]]$key$key_offsets
|
||||
# I think the integer output indices are stored as variable-length (in bytes)
|
||||
# data objects.
|
||||
mean.size.one.ring.member <- mean.size.16.ring.input / 16
|
||||
|
||||
|
||||
|
||||
prunable.bpp <- function(x) {
|
||||
x <- cut(x, breaks = c(0, 2, 4, 8, 16), labels = c("7", "8", "9", "10"))
|
||||
x <- 32 * 2 * as.numeric(as.character(x))
|
||||
# For L and R
|
||||
# Two outputs: 32 * 2 * 7
|
||||
# 3-4 outputs: 32 * 2 * 8
|
||||
# 5-8 outputs: 32 * 2 * 9
|
||||
# 9-16 outputs: 32 * 2 * 10
|
||||
# (Times 2 since there is one 32-byte string each for L and R)
|
||||
x + 32 * 6
|
||||
# 32 * 6 because there are 32 bytes each for A, A1, B, r1, s1, and d1
|
||||
}
|
||||
|
||||
|
||||
|
||||
|
||||
C_u <- function(f, n) {
|
||||
|
||||
ring.size.sim <- n
|
||||
|
||||
non.spam.fingerprint.tx.sim.tabulated.weight[, tx_weight_bytes.sim :=
|
||||
N * (tx_weight_bytes - mean.size.16.ring.input * number_of_inputs +
|
||||
number_of_inputs * mean.size.one.ring.member * ring.size.sim)]
|
||||
|
||||
mean.non.spam.kb.per.block <-
|
||||
(sum(non.spam.fingerprint.tx.sim.tabulated.weight[, tx_weight_bytes.sim])/num.blocks.before.spam)
|
||||
# Coinbase txs are excluded
|
||||
|
||||
mean.non.spam.kb.per.block * f
|
||||
|
||||
}
|
||||
|
||||
|
||||
|
||||
|
||||
usd.xmr.rate <- 120 # April 2024 exchange rate
|
||||
n.nodes <- 22537 # From monero.fail/map April 2024
|
||||
ssd.1.tb.usd <- 114.50 # Median price of 1 TB SATA SSD April 2024 https://ssd.userbenchmark.com/
|
||||
|
||||
C_d <- function(n, m) {
|
||||
|
||||
tb <- 1e+12
|
||||
|
||||
ring.size.sim <- n
|
||||
|
||||
non.spam.fingerprint.tx.sim.tabulated.size[, tx_size_bytes.sim :=
|
||||
N * (tx_size_bytes - mean.size.16.ring.input * number_of_inputs + number_of_inputs * mean.size.one.ring.member * ring.size.sim)]
|
||||
|
||||
mean.non.spam.kb.per.block <- mean.coinbase.tx.size +
|
||||
(sum(non.spam.fingerprint.tx.sim.tabulated.size[, tx_size_bytes.sim])/num.blocks.before.spam)
|
||||
# Keep coinbase tx since that has to be stored
|
||||
|
||||
bytes <- mean.non.spam.kb.per.block
|
||||
|
||||
m * bytes * n.nodes * (ssd.1.tb.usd / usd.xmr.rate) / tb
|
||||
|
||||
}
|
||||
|
||||
C_u <- Vectorize(C_u)
|
||||
C_d <- Vectorize(C_d)
|
||||
# Have to Vectorize() these because otherwise the arguments will be
|
||||
# expanded as vectors incorrectly when working on the blockchain dataset
|
||||
|
||||
|
||||
ref.tx.size.cost <- function(f, n) {
|
||||
|
||||
stopifnot(length(f) == length(n))
|
||||
|
||||
tx.size <- non.spam.fingerprint.tx.sim[number_of_inputs == 2 & number_of_outputs == 2,
|
||||
mean(tx_size_bytes) - mean.size.16.ring.input * 2 + 2 * mean.size.one.ring.member * n]
|
||||
|
||||
tx.weight <- non.spam.fingerprint.tx.sim[number_of_inputs == 2 & number_of_outputs == 2,
|
||||
mean(tx_weight_bytes) - mean.size.16.ring.input * 2 + 2 * mean.size.one.ring.member * n]
|
||||
|
||||
list(size = tx.size, cost = tx.weight * f * usd.xmr.rate)
|
||||
|
||||
}
|
||||
|
||||
# No need to Vectorize() ref.tx.size.cost()
|
||||
|
||||
|
||||
|
||||
stopifnot(ceiling(mean.size.zero.ring.tx.size) == 975)
|
||||
stopifnot(ceiling(mean.size.one.ring.member) == 35)
|
||||
|
||||
adversary.owned.outputs <- function(b, f, n) {
|
||||
2 * b / (f * (975 + 35 * n))
|
||||
}
|
||||
|
||||
eff.ring.size <- function(b, f, n) {
|
||||
1 + (n - 1) * r /
|
||||
(r + adversary.owned.outputs(b, f, n) )
|
||||
}
|
||||
|
||||
adversary.share.outputs <- function(b, f, n) {
|
||||
1 - r /
|
||||
(r + adversary.owned.outputs(b, f, n) )
|
||||
}
|
||||
|
||||
|
||||
CE <- function(f, n, m, b) {
|
||||
(C_u(f, n) + C_d(n, m)) /
|
||||
eff.ring.size(b, f, n)
|
||||
}
|
||||
# Cost effectiveness
|
||||
|
||||
|
||||
|
||||
|
||||
f.range <- seq(0.000000010, 0.000000020 * 20, length.out = 40)
|
||||
n.range <- seq(11, 60, by = 1)
|
||||
f.n.range <- expand.grid(f = f.range, n = n.range)
|
||||
|
||||
min.acceptable.eff.ring.size <- 5
|
||||
|
||||
|
||||
status.quo.no.attack.block.size <- C_u(1, 16)
|
||||
status.quo.no.attack.block.size.one.year <-
|
||||
status.quo.no.attack.block.size * 30 * 24 * 365 / 10^9
|
||||
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out[, prunable.data :=
|
||||
N * (number_of_inputs * (32 * 3 + 32 * 16) + prunable.bpp(number_of_outputs) ) ]
|
||||
|
||||
prunable.data.per.block <- sum(non.spam.fingerprint.tx.sim.tabulated.in.out$prunable.data)/num.blocks.before.spam
|
||||
|
||||
status.quo.no.attack.block.size.one.year.pruned <-
|
||||
(status.quo.no.attack.block.size - (7/8) * prunable.data.per.block) * 30 * 24 * 365 / 10^9
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
perf.tests <- readLines("performance-test/CLSAG-performance.txt")
|
||||
|
||||
skip <- grep("CLSAG", perf.tests)[1] - 1
|
||||
|
||||
perf.tests <- read.csv("performance-test/CLSAG-performance.txt", skip = skip, header = FALSE, stringsAsFactors = FALSE)
|
||||
|
||||
header.names <- c("CLSAG", "tx_size", "batch_size", "rangeproof_splits", "inputs", "outputs", "decomp_n", "decomp_m", "ring_size",
|
||||
"test_name",
|
||||
"posix_time", "iterations",
|
||||
"min", "max", "mean", "med", "stddev", "npskew")
|
||||
|
||||
perf.tests <- perf.tests[, 1:length(header.names)]
|
||||
# Remove quantile data
|
||||
colnames(perf.tests) <- header.names
|
||||
|
||||
stopifnot(all(perf.tests$ring_size == perf.tests$decomp_n ^ perf.tests$decomp_m))
|
||||
|
||||
|
||||
perf.tests$mean <- 10^-6 * perf.tests$mean # Convert from nanoseconds to milliseconds
|
||||
|
||||
pow.of.two <- 2^(1:4)
|
||||
|
||||
|
||||
summary(perf.model.short <- lm(mean ~ ring_size * inputs + factor(ceiling(log2(outputs))), data = perf.tests))
|
||||
summary(perf.model.long <- lm(mean ~ ring_size * inputs + log2(ring_size) * log2(inputs) + factor(ceiling(log2(outputs))), data = perf.tests))
|
||||
|
||||
nested.model.test <- anova(perf.model.short, perf.model.long, test = "F")
|
||||
|
||||
print(nested.model.test)
|
||||
|
||||
stopifnot(nested.model.test[["Pr(>F)"]][2] == 0)
|
||||
# nested.model.test[["Pr(>F)"]][2] == 0 means p value is < 2.2e-16
|
||||
|
||||
|
||||
|
||||
|
||||
alice.best.response <- function(b, f.n.range, m = 2, min.acceptable.eff.ring.size = 5, force.eval.point = NULL, plot = TRUE) {
|
||||
|
||||
b <- b / (24*30)
|
||||
# Convert to budget per block
|
||||
|
||||
|
||||
if ( ! is.null(force.eval.point)) {
|
||||
|
||||
if (plot == TRUE) {
|
||||
stop("Cannot force.eval.point and plot at the same time.")
|
||||
}
|
||||
|
||||
stopifnot(is.data.frame(force.eval.point))
|
||||
stopifnot(all(colnames(force.eval.point) == c("f", "n")))
|
||||
|
||||
|
||||
contour.contents <- CE(force.eval.point$f, force.eval.point$n, m, b)
|
||||
contour.contents <- contour.contents * 1000 # Convert to millineros
|
||||
cost.effectiveness.at.optimum <- contour.contents
|
||||
|
||||
unrestricted.min <- force.eval.point
|
||||
restricted.min <- force.eval.point
|
||||
eff.ring.size.at.optimum <- eff.ring.size(b, force.eval.point$f, force.eval.point$n)
|
||||
|
||||
|
||||
|
||||
} else {
|
||||
|
||||
|
||||
contour.contents <- CE(f.n.range$f, f.n.range$n, m, b)
|
||||
contour.contents <- contour.contents * 1000 # Convert to millineros
|
||||
contour.matrix <- matrix(contour.contents, nrow = length(f.range), byrow = FALSE)
|
||||
|
||||
eff.ring.size.evaluated <- eff.ring.size(b, f.n.range$f, f.n.range$n)
|
||||
|
||||
unrestricted.min <- f.n.range[which.min(contour.contents), ]
|
||||
|
||||
restricted.min <- f.n.range[
|
||||
eff.ring.size.evaluated >= min.acceptable.eff.ring.size, ][
|
||||
which.min(contour.contents[eff.ring.size.evaluated >= min.acceptable.eff.ring.size]), ]
|
||||
|
||||
eff.ring.size.at.optimum <- eff.ring.size.evaluated[
|
||||
eff.ring.size.evaluated >= min.acceptable.eff.ring.size][
|
||||
which.min(contour.contents[eff.ring.size.evaluated >= min.acceptable.eff.ring.size])]
|
||||
|
||||
cost.effectiveness.at.optimum <- contour.contents[f.n.range$f == restricted.min$f & f.n.range$n == restricted.min$n]
|
||||
|
||||
}
|
||||
|
||||
if (nrow(restricted.min) == 0) {
|
||||
stop("Constraint set is empty. This means no values in f.n.range satisfied the min.acceptable.eff.ring.size.")
|
||||
}
|
||||
|
||||
|
||||
attack.block.size.at.restricted.min <-
|
||||
C_u(restricted.min[, "f"], restricted.min[, "n"]) / restricted.min[, "f"] + # Data contributed by normal users
|
||||
b / restricted.min[, "f"] # Data contributed by adversary
|
||||
|
||||
no.attack.block.size.at.restricted.min <-
|
||||
C_u(restricted.min[, "f"], restricted.min[, "n"]) / restricted.min[, "f"]
|
||||
|
||||
no.attack.block.size.at.restricted.min.one.year <-
|
||||
no.attack.block.size.at.restricted.min * 30 * 24 * 365 / 10^9
|
||||
|
||||
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out[, prunable.data :=
|
||||
N * (number_of_inputs * (32 * 3 + 32 * restricted.min[, "n"]) + prunable.bpp(number_of_outputs) ) ]
|
||||
# TODO: explain this computation
|
||||
|
||||
prunable.data.per.block <- sum(non.spam.fingerprint.tx.sim.tabulated.in.out$prunable.data)/num.blocks.before.spam
|
||||
|
||||
|
||||
no.attack.block.size.at.restricted.min.one.year <- no.attack.block.size.at.restricted.min * 30 * 24 * 365 / 10^9
|
||||
no.attack.block.size.at.restricted.min.one.year.pruned <-
|
||||
(no.attack.block.size.at.restricted.min - (7/8) * prunable.data.per.block) * 30 * 24 * 365 / 10^9
|
||||
# TODO: explain this computation
|
||||
|
||||
attack.block.size.at.restricted.min.one.year <- attack.block.size.at.restricted.min * 30 * 24 * 365 / 10^9
|
||||
|
||||
|
||||
n.adversary.tx.per.block <- adversary.owned.outputs(b, restricted.min[, "f"], restricted.min[, "n"]) / 2
|
||||
|
||||
prunable.data.per.block.adversary <- n.adversary.tx.per.block * (1 * (32 * 3 + 32 * restricted.min[, "n"]) + prunable.bpp(2) )
|
||||
# TODO: explain this computation
|
||||
|
||||
attack.block.size.at.restricted.min.one.year.pruned <-
|
||||
(attack.block.size.at.restricted.min - (7/8) * (prunable.data.per.block + prunable.data.per.block.adversary)) * 30 * 24 * 365 / 10^9
|
||||
# TODO: explain this computation
|
||||
|
||||
ref.tx.at.optimum <- ref.tx.size.cost(restricted.min[, "f"], restricted.min[, "n"])
|
||||
|
||||
predicted.verif.time.ref.tx <- predict(perf.model.long,
|
||||
newdata = data.frame(inputs = 2, outputs = 2, ring_size = restricted.min[, "n"]))
|
||||
|
||||
|
||||
predicted.verif.time.normal.block <- predict(perf.model.long,
|
||||
newdata = non.spam.fingerprint.tx.sim.tabulated.in.out[,
|
||||
.(inputs = number_of_inputs, outputs = number_of_outputs, ring_size = restricted.min[, "n"])])
|
||||
|
||||
predicted.verif.time.normal.block <- sum(predicted.verif.time.normal.block *
|
||||
non.spam.fingerprint.tx.sim.tabulated.in.out$N) / num.blocks.before.spam
|
||||
|
||||
|
||||
predicted.verif.time.spam.part.block <- n.adversary.tx.per.block * predict(perf.model.long,
|
||||
newdata = data.frame(inputs = 1, outputs = 2, ring_size = restricted.min[, "n"]))
|
||||
|
||||
|
||||
# Adversary budget, ring_size, fee_per_byte, effective_ring_size,
|
||||
# User's cost for 2in/2out tx,, User's tx size for 2in/2out tx,
|
||||
# Block size (no attack), Block size (attack),
|
||||
# One year blockchain growth (unpruned, no attack), One year blockchain growth (unpruned, attack),
|
||||
# One year blockchain growth (pruned, no attack), One year blockchain growth (pruned, attack)
|
||||
|
||||
results.table <- data.table(
|
||||
b = b, b_per_day = b * 30 * 24,
|
||||
ring_size = restricted.min[, "n"], fee_per_byte = restricted.min[, "f"] * 10^9,
|
||||
cost_effectiveness = cost.effectiveness.at.optimum,
|
||||
effective_ring_size = eff.ring.size(b, restricted.min[, "f"], restricted.min[, "n"]),
|
||||
user_tx_cost_2in_2out = ref.tx.at.optimum$cost, user_tx_size_2in_2out = ref.tx.at.optimum$size,
|
||||
block_size_no_attack = no.attack.block.size.at.restricted.min,
|
||||
block_size_attack = attack.block.size.at.restricted.min,
|
||||
one_year_blockchain_growth_unpruned_no_attack = no.attack.block.size.at.restricted.min.one.year,
|
||||
one_year_blockchain_growth_unpruned_attack = attack.block.size.at.restricted.min.one.year,
|
||||
one_year_blockchain_growth_pruned_no_attack = no.attack.block.size.at.restricted.min.one.year.pruned,
|
||||
one_year_blockchain_growth_pruned_attack = attack.block.size.at.restricted.min.one.year.pruned,
|
||||
verif_time_2in_2out = predicted.verif.time.ref.tx * 10^-3, # Times 10^-3 converts to seconds
|
||||
verif_time_no_attack = predicted.verif.time.normal.block * 10^-3,
|
||||
verif_time_attack = (predicted.verif.time.normal.block + predicted.verif.time.spam.part.block)* 10^-3
|
||||
)
|
||||
|
||||
|
||||
|
||||
if (! plot) {
|
||||
return(results.table)
|
||||
}
|
||||
|
||||
|
||||
|
||||
par(mar = c(10, 4, 4, 2) + 0.1)
|
||||
|
||||
filled.contour(x = f.range, y = n.range, z = contour.matrix,
|
||||
main = paste0("Most cost-effective minimum fee and ring size, given adversary budget of ",
|
||||
round(b * 24*30, 2), " XMR/day"),
|
||||
# TODO list adversary budget in title
|
||||
ylab = "Nominal ring size",
|
||||
key.title = title(main = "Cost\nEffectiveness\n(lower is better)",
|
||||
cex.main = 1, font.main = 1, xpd = NA),
|
||||
# non-bold font. xpd = NA means that title isn't clipped.
|
||||
ylim = c(min(n.range) - 1, max(n.range) + 1),
|
||||
xlim = c(min(f.range) - mean(f.range) * 0.05, max(f.range) + mean(f.range) * 0.05),
|
||||
plot.axes = {
|
||||
mtext(side = 1, line = 8.5, adj = 0,
|
||||
text =
|
||||
paste0("Adversary XMR budget per day: ", round(b * 24*30, 2),
|
||||
"\nEffective ring size: ", round(eff.ring.size.at.optimum, 2),
|
||||
", Adversary share of outputs: ", round(adversary.share.outputs(b, restricted.min[, "f"], restricted.min[, "n"]), 2),
|
||||
"\nAggregate XMR cost to transacting users per block: " , round(C_u(restricted.min[, "f"], restricted.min[, "n"]), 3),
|
||||
"\nAggregate XMR cost to node operators per block with normal tx volume: ", round(C_d(restricted.min[, "n"], m), 3),
|
||||
"\n2in/2out tx size at optimum: ", round(ref.tx.at.optimum$size, 0),
|
||||
" bytes, 2in/2out tx cost at optimum: ", round(ref.tx.at.optimum$cost * 100, 2), " USD cents",
|
||||
"\nOne year blockchain growth with normal tx volume unpruned: ",
|
||||
round(no.attack.block.size.at.restricted.min.one.year), " GB, pruned: ",
|
||||
round(no.attack.block.size.at.restricted.min.one.year.pruned), " GB",
|
||||
" github.com/Rucknium"))
|
||||
legend("bottomright",
|
||||
legend = c("Optimal fee and ring size, unrestricted", "Optimal fee and ring size, restricted",
|
||||
"Minimum acceptable effective ring size"), xpd = NA, inset = c(-0.175, -0.15),
|
||||
pch = c(17, 16, NA), lty = c(NA, NA, 1),
|
||||
col = c("blue", "green4", "black"), pt.cex = c(2, 4, NA), lwd = 2, cex = 1.1)
|
||||
title(xlab = "Minimum fee (nanoneros per byte)", line = 2.25)
|
||||
x.axis.ticks <- seq(min(f.range), max(f.range), by = 2e-08)
|
||||
axis(1, at = x.axis.ticks, labels = x.axis.ticks * 10^9)
|
||||
axis(2)
|
||||
contour.contents.2 <- eff.ring.size(b, f.n.range$f, f.n.range$n)
|
||||
contour.matrix.2 <- matrix(contour.contents.2, nrow = length(f.range), byrow = FALSE)
|
||||
contour(x = f.range, y = n.range, z = contour.matrix.2, method = "edge",
|
||||
levels = min.acceptable.eff.ring.size, vfont = c("sans serif", "bold"),
|
||||
labcex = 1.75, add = TRUE)
|
||||
|
||||
points(restricted.min, pch = 16, col = "green4", cex = 4)
|
||||
points(unrestricted.min, pch = 17, col = "blue", cex = 2)
|
||||
|
||||
}
|
||||
)
|
||||
|
||||
return(results.table)
|
||||
|
||||
}
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
library(gt)
|
||||
|
||||
|
||||
|
||||
latex.table <- function(x, title = NULL, col.widths, output = "", label = "", source.note = NULL, add.row.color = NULL) {
|
||||
|
||||
stopifnot(ncol(x) == length(col.widths))
|
||||
|
||||
latex.output <- as.data.frame(x) |>
|
||||
gt() |>
|
||||
cols_label(
|
||||
b_per_day = "Adversary XMR budget per day",
|
||||
ring_size = "Nominal ring size",
|
||||
fee_per_byte = "Min fee (nanoneros per byte)",
|
||||
cost_effectiveness = "CE",
|
||||
effective_ring_size = "Effective ring size",
|
||||
user_tx_size_2in_2out = "Size of 2in/2out (bytes)",
|
||||
user_tx_cost_2in_2out = "User's cost to send 2in/2out (USD cents)",
|
||||
block_size_no_attack = "Block size (KB)",
|
||||
block_size_attack = "Block size (KB)",
|
||||
one_year_blockchain_growth_unpruned_no_attack = "Unpruned",
|
||||
one_year_blockchain_growth_unpruned_attack = "Unpruned",
|
||||
one_year_blockchain_growth_pruned_no_attack = "Pruned",
|
||||
one_year_blockchain_growth_pruned_attack = "Pruned",
|
||||
verif_time_2in_2out = "Seconds to verify 2in/2out",
|
||||
verif_time_no_attack = "Seconds to verify txs in block",
|
||||
verif_time_attack = "Seconds to verify txs in block"
|
||||
) |>
|
||||
fmt_number(columns = matches("(blockchain)|(fee_per_byte)|(block_size)|(user_tx_size_2in_2out)"), decimals = 0) |>
|
||||
fmt_number(columns = matches("(b_per_day)|(effective_ring_size)|(user_tx_cost)|(verif_time_no_attack)|(verif_time_attack)|(cost_effectiveness)"), decimals = 2) |>
|
||||
fmt_number(columns = matches("(verif_time_2in_2out)"), decimals = 3) |>
|
||||
tab_header(title = title) |>
|
||||
tab_spanner(label = "One year blockchain growth (GB)", columns = starts_with("one_year_blockchain_growth")) |>
|
||||
tab_spanner(label = "Normal tx volume", columns = matches("no_attack")) |>
|
||||
tab_spanner(label = "Normal tx volume + black marble flooding", columns = matches("([^n][^o]_attack)|(effective_ring_size)")) |>
|
||||
# "we build spanners from the bottom up" https://gt.rstudio.com/reference/tab_spanner.html
|
||||
tab_source_note(source_note = source.note)
|
||||
|
||||
if (! is.null(add.row.color)) {
|
||||
latex.output <- latex.output |>
|
||||
data_color(columns = everything(), rows = add.row.color$row, fn = function(x) add.row.color$color)
|
||||
}
|
||||
|
||||
latex.output <- latex.output |>
|
||||
as_latex() |>
|
||||
as.character()
|
||||
|
||||
latex.output <- gsub("begin[{]longtable[}][{][^\n]+",
|
||||
paste0("begin{longtable}{", paste0("Rp{", col.widths, "cm}", collapse = ""), "}"),
|
||||
latex.output)
|
||||
|
||||
latex.output <- gsub("caption*", "caption", latex.output, fixed = TRUE)
|
||||
# Removing the "*" means that the table is numbered in the final PDF output
|
||||
|
||||
latex.output <- gsub("\\end{longtable}",
|
||||
paste0("\\label{", label, "}\n\\end{longtable}"), latex.output, fixed = TRUE)
|
||||
|
||||
|
||||
cat(latex.output, file = output)
|
||||
|
||||
invisible(NULL)
|
||||
|
||||
}
|
||||
|
||||
|
||||
|
||||
permuted.options <- expand.grid(f = c(10, 20, 40, 100, 200) * 10^-9, n = c(16, 30, 45, 60))
|
||||
|
||||
results.table <- list()
|
||||
|
||||
for (i in seq_len(nrow(permuted.options))) {
|
||||
results.table[[i]] <- alice.best.response(b = 2.5, f.n.range = f.n.range,
|
||||
force.eval.point = permuted.options[i, ], plot = FALSE)
|
||||
}
|
||||
|
||||
results.table <- data.table::rbindlist(results.table)
|
||||
|
||||
|
||||
|
||||
|
||||
latex.table(results.table[, .(
|
||||
b_per_day, ring_size, fee_per_byte, cost_effectiveness,
|
||||
user_tx_size_2in_2out = user_tx_size_2in_2out,
|
||||
user_tx_cost_2in_2out = user_tx_cost_2in_2out * 100,
|
||||
verif_time_2in_2out,
|
||||
block_size_no_attack = block_size_no_attack / 1000,
|
||||
verif_time_no_attack,
|
||||
one_year_blockchain_growth_unpruned_no_attack,
|
||||
one_year_blockchain_growth_pruned_no_attack,
|
||||
one_year_blockchain_growth_unpruned_attack,
|
||||
one_year_blockchain_growth_pruned_attack,
|
||||
effective_ring_size,
|
||||
block_size_attack = block_size_attack / 1000,
|
||||
verif_time_attack
|
||||
)],
|
||||
title = "Cost effectiveness of minimum fee and ring size options when adversary budget is 2.5 XMR per day",
|
||||
output = "tables/permuted-cost-effectiveness-2_5-budget.tex",
|
||||
label = "table-2_5-budget",
|
||||
col.widths = c(1.75, 1, 1.5, 0.75, 1, 2, 1.5, 0.75, 1.4, 1, 1, 1, 1, 1, 0.75, 1.4),
|
||||
source.note = "Row in green is the status quo. Row in orange is the best cost effectiveness.",
|
||||
add.row.color =
|
||||
data.frame(row = c(2, which.min(results.table$cost_effectiveness)), color = c("green", "orange")))
|
||||
|
||||
|
||||
|
||||
|
||||
b.options <- 2.5 * c(0.1, 0.2, 0.5, 1, 2, 5, 10, 20, 50, 100, 200)
|
||||
|
||||
results.table <- list()
|
||||
|
||||
results.table[[1]] <- alice.best.response(b = 2.5, f.n.range = f.n.range,
|
||||
force.eval.point = data.frame(f = 20 * 10^-9, n = 16), plot = FALSE)
|
||||
|
||||
for (i in seq_along(b.options)) {
|
||||
results.table[[i + 1]] <- alice.best.response(b = b.options[i], f.n.range = f.n.range, plot = FALSE)
|
||||
}
|
||||
|
||||
results.table <- data.table::rbindlist(results.table)
|
||||
|
||||
|
||||
|
||||
latex.table(results.table[, .(
|
||||
b_per_day, ring_size, fee_per_byte, cost_effectiveness,
|
||||
user_tx_size_2in_2out = user_tx_size_2in_2out,
|
||||
user_tx_cost_2in_2out = user_tx_cost_2in_2out * 100,
|
||||
verif_time_2in_2out,
|
||||
block_size_no_attack = block_size_no_attack / 1000,
|
||||
verif_time_no_attack,
|
||||
one_year_blockchain_growth_unpruned_no_attack,
|
||||
one_year_blockchain_growth_pruned_no_attack,
|
||||
one_year_blockchain_growth_unpruned_attack,
|
||||
one_year_blockchain_growth_pruned_attack,
|
||||
effective_ring_size,
|
||||
block_size_attack = block_size_attack / 1000,
|
||||
verif_time_attack
|
||||
)],
|
||||
title = "Minimum fee and ring size at optimal cost effectiveness, adversary budget scenarios",
|
||||
output = "tables/cost-effectiveness-budget-scenarios.tex",
|
||||
label = "table-scenarios-budget",
|
||||
col.widths = c(1.75, 1, 1.5, 0.75, 1, 2, 1.5, 0.75, 1.4, 1, 1, 1, 1, 1, 0.75, 1.4),
|
||||
source.note = "Row in green is the status quo",
|
||||
add.row.color = data.frame(row = 1, color = "green"))
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
# make plot
|
||||
png(paste0("images/cost-effective-contour-plot-50-budget.png"), width = 800, height = 900)
|
||||
alice.best.response(b = 50, f.n.range = f.n.range, plot = TRUE)
|
||||
dev.off()
|
||||
|
||||
|
||||
# make animation
|
||||
library(animation)
|
||||
library(Cairo)
|
||||
|
||||
# If Cairo is installed, use:
|
||||
ani.options(interval = 2, ani.dev = "CairoPNG",
|
||||
ani.width = 800, ani.height = 900)
|
||||
# Otherwise, use:
|
||||
# ani.options(interval = 2, ani.width = 800, ani.height = 900)
|
||||
|
||||
saveGIF({
|
||||
for (i in seq_along(b.options)) {
|
||||
alice.best.response(b = b.options[i], f.n.range = f.n.range, plot = TRUE)
|
||||
}
|
||||
}, movie.name = "cost-effectiveness-animation.gif")
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
library(huxtable)
|
||||
|
||||
# report_latex_dependencies()
|
||||
|
||||
replacement.names <- names(coef(perf.model.long))
|
||||
names(replacement.names) <- replacement.names
|
||||
names(replacement.names) <- gsub(":", " $\\times$ ", names(replacement.names), fixed = TRUE)
|
||||
names(replacement.names) <- gsub("factor(ceiling(log2(outputs)))",
|
||||
"$\\lceil\\log_{2}(\\mathrm{outputs})\\rceil = $ ", names(replacement.names), fixed = TRUE)
|
||||
|
||||
names(replacement.names) <- gsub("log2",
|
||||
"$\\log_{2}$", names(replacement.names), fixed = TRUE)
|
||||
|
||||
|
||||
names(replacement.names) <- gsub("ring_", "ring ", names(replacement.names), fixed = TRUE)
|
||||
|
||||
|
||||
perf.model.long.tex <- huxreg(perf.model.long, error_pos = "same",
|
||||
statistics = c(N = "nobs", `Adjusted R-squared` = "adj.r.squared"),
|
||||
coefs = replacement.names,
|
||||
note = "Standard errors in parentheses. {stars}.")
|
||||
# generics::glance(perf.model.long)
|
||||
|
||||
perf.model.long.tex.n.rows <- nrow(number_format(perf.model.long.tex))
|
||||
number_format(perf.model.long.tex)[perf.model.long.tex.n.rows - 1, 2] <- "%.4f"
|
||||
# number_format = "%.4f" so that the R^2 does not display as just rounded "1"
|
||||
perf.model.long.tex <- set_escape_contents(perf.model.long.tex,
|
||||
row = seq_len(length(replacement.names) + 1), value = FALSE)
|
||||
# Don't excape the Latex statements
|
||||
|
||||
perf.model.long.tex <- to_latex(perf.model.long.tex, tabular_only = TRUE)
|
||||
|
||||
cat(perf.model.long.tex, file = "tables/verification-time-regression.tex")
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
# P2Pool calculations
|
||||
|
||||
coinbase.outputs.per.block <- output.index[tx_num == 1, .N / num.blocks.before.spam]
|
||||
# output.index[tx_num != 1, .N / num.blocks.before.spam]
|
||||
|
||||
print(coinbase.outputs.per.block * 30 * 24 * 356 * mean.size.one.ring.member * 59 / 1e+9)
|
||||
# If coinbase consolations are ring size 1, then we have 2.7 GB less data in a year
|
||||
|
||||
# "Coinbase Consolidation Tx Type"
|
||||
# https://github.com/monero-project/research-lab/issues/108
|
||||
# "Avoid selecting coinbase outputs as decoys"
|
||||
# https://github.com/monero-project/research-lab/issues/109
|
||||
|
||||
|
||||
|
||||
tenth.percentile.p2pool.output.amounts <- output.index[
|
||||
tx_num == 1 & 10^-12 * output_amount < 0.6, 10^-12 * quantile(output_amount, probs = 0.1)]
|
||||
|
||||
print( ( (32 * 4 + mean.size.one.ring.member * 16) * 20 * 1e-09) / tenth.percentile.p2pool.output.amounts )
|
||||
# status quo: A ring consumes 5% of the coinbase output in fees
|
||||
|
||||
print( ( (32 * 4 + mean.size.one.ring.member * 60) * 70 * 1e-09) / tenth.percentile.p2pool.output.amounts )
|
||||
# Ring size 60 and 60 nanoneros / byte fee: A ring consumes 49% of the coinbase output in fees
|
||||
|
||||
print( ( (32 * 4 + mean.size.one.ring.member * 1) * 70 * 1e-09) / tenth.percentile.p2pool.output.amounts )
|
||||
# Ring size 1 and 60 nanoneros / byte fee: A ring consumes 3.6% of the coinbase output in fees
|
||||
|
||||
|
||||
|
||||
output.index[
|
||||
tx_num == 1 & 10^-12 * output_amount < 0.6, 10^-12 * quantile(output_amount, probs = 0.1)]
|
||||
|
||||
|
||||
324
Monero-Black-Marble-Flood/code/tradeoff-output-index.R
Normal file
324
Monero-Black-Marble-Flood/code/tradeoff-output-index.R
Normal file
|
|
@ -0,0 +1,324 @@
|
|||
|
||||
|
||||
# Install packages:
|
||||
# install.packages(c("ggplot2", "data.table", "RJSONIO", "RCurl", "parallelly", "future", "future.apply", "huxtable", "gt", "animation", "Cairo"))
|
||||
# Cairo is helpful, but not necessary
|
||||
|
||||
|
||||
library(data.table)
|
||||
|
||||
|
||||
|
||||
current.height <- 3097307
|
||||
# Last block of March 4, 2024 UTC
|
||||
# current.height should be the most recent height that you want to collect data for
|
||||
start.height <- 3077201
|
||||
# First block of February 5, 2024 UTC
|
||||
|
||||
url.rpc <- "http://127.0.0.1:18081"
|
||||
# Set the IP address and port of your node. Should usually be "http://127.0.0.1:18081"
|
||||
|
||||
|
||||
stopifnot(!is.na(current.height))
|
||||
|
||||
block.heights <- start.height:current.height
|
||||
|
||||
|
||||
|
||||
|
||||
# Modified from TownforgeR::tf_rpc_curl function
|
||||
xmr.rpc <- function(
|
||||
url.rpc = "http://127.0.0.1:18081/json_rpc",
|
||||
method = "",
|
||||
params = list(),
|
||||
userpwd = "",
|
||||
num.as.string = FALSE,
|
||||
nonce.as.string = FALSE,
|
||||
keep.trying.rpc = FALSE,
|
||||
curl = RCurl::getCurlHandle(),
|
||||
...
|
||||
){
|
||||
|
||||
json.ret <- RJSONIO::toJSON(
|
||||
list(
|
||||
jsonrpc = "2.0",
|
||||
id = "0",
|
||||
method = method,
|
||||
params = params
|
||||
), digits = 50
|
||||
)
|
||||
|
||||
rcp.ret <- tryCatch(RCurl::postForm(url.rpc,
|
||||
.opts = list(
|
||||
userpwd = userpwd,
|
||||
postfields = json.ret,
|
||||
httpheader = c('Content-Type' = 'application/json', Accept = 'application/json')
|
||||
# https://stackoverflow.com/questions/19267261/timeout-while-reading-csv-file-from-url-in-r
|
||||
),
|
||||
curl = curl
|
||||
), error = function(e) {NULL})
|
||||
|
||||
if (keep.trying.rpc && length(rcp.ret) == 0) {
|
||||
while (length(rcp.ret) == 0) {
|
||||
rcp.ret <- tryCatch(RCurl::postForm(url.rpc,
|
||||
.opts = list(
|
||||
userpwd = userpwd,
|
||||
postfields = json.ret,
|
||||
httpheader = c('Content-Type' = 'application/json', Accept = 'application/json')
|
||||
# https://stackoverflow.com/questions/19267261/timeout-while-reading-csv-file-from-url-in-r
|
||||
),
|
||||
curl = curl
|
||||
), error = function(e) {NULL})
|
||||
}
|
||||
}
|
||||
|
||||
if (is.null(rcp.ret)) {
|
||||
stop("Cannot connect to monerod. Is monerod running?")
|
||||
}
|
||||
|
||||
if (num.as.string) {
|
||||
rcp.ret <- gsub("(: )([-0123456789.]+)([,\n\r])", "\\1\"\\2\"\\3", rcp.ret )
|
||||
}
|
||||
|
||||
if (nonce.as.string & ! num.as.string) {
|
||||
rcp.ret <- gsub("(\"nonce\": )([-0123456789.]+)([,\n\r])", "\\1\"\\2\"\\3", rcp.ret )
|
||||
}
|
||||
|
||||
RJSONIO::fromJSON(rcp.ret, asText = TRUE) # , simplify = FALSE
|
||||
}
|
||||
|
||||
|
||||
|
||||
system.time({
|
||||
|
||||
n.workers <- min(floor(parallelly::availableCores()/2), 32L)
|
||||
|
||||
future::plan(future::multisession(workers = n.workers))
|
||||
options(future.globals.maxSize= 8000*1024^2)
|
||||
|
||||
set.seed(314)
|
||||
|
||||
# Randomize block heights to make processing time more uniform between parallel processes
|
||||
block.heights <- split(block.heights, sample(cut(block.heights, n.workers)))
|
||||
# First randomly put heights into list elements (split() will sort them ascendingly in each list element)
|
||||
block.heights <- lapply(block.heights, sample)
|
||||
# Then order the heights randomly within each list element
|
||||
block.heights <- unname(block.heights)
|
||||
|
||||
returned <- future.apply::future_lapply(block.heights, function(block.heights) {
|
||||
|
||||
handle <- RCurl::getCurlHandle()
|
||||
|
||||
return.data <- vector("list", length(block.heights))
|
||||
|
||||
for (height.iter in seq_along(block.heights)) {
|
||||
|
||||
height <- block.heights[height.iter]
|
||||
|
||||
block.data <- xmr.rpc(url.rpc = paste0(url.rpc, "/json_rpc"),
|
||||
method = "get_block",
|
||||
params = list(height = height ),
|
||||
keep.trying.rpc = TRUE,
|
||||
curl = handle)$result
|
||||
|
||||
txs.to.collect <- c(block.data$miner_tx_hash, block.data$tx_hashes)
|
||||
|
||||
rcp.ret <- tryCatch(RCurl::postForm(paste0(url.rpc, "/get_transactions"),
|
||||
.opts = list(
|
||||
postfields = paste0('{"txs_hashes":["', paste0(txs.to.collect, collapse = '","'), '"],"decode_as_json":true}'),
|
||||
httpheader = c('Content-Type' = 'application/json', Accept = 'application/json')
|
||||
),
|
||||
curl = handle
|
||||
), error = function(e) {NULL})
|
||||
|
||||
if (length(rcp.ret) == 0) {
|
||||
while (length(rcp.ret) == 0) {
|
||||
rcp.ret <- tryCatch(RCurl::postForm(paste0(url.rpc, "/get_transactions"),
|
||||
.opts = list(
|
||||
postfields = paste0('{"txs_hashes":["', paste0(txs.to.collect, collapse = '","'), '"],"decode_as_json":true}'),
|
||||
httpheader = c('Content-Type' = 'application/json', Accept = 'application/json')
|
||||
),
|
||||
curl = handle
|
||||
), error = function(e) {NULL})
|
||||
}
|
||||
}
|
||||
|
||||
rcp.ret <- RJSONIO::fromJSON(rcp.ret, asText = TRUE)
|
||||
|
||||
output.index.collected <- vector("list", length(txs.to.collect))
|
||||
rings.collected <- vector("list", length(txs.to.collect) - 1)
|
||||
|
||||
for (i in seq_along(txs.to.collect)) {
|
||||
|
||||
tx.json <- tryCatch(
|
||||
RJSONIO::fromJSON(rcp.ret$txs[[i]]$as_json, asText = TRUE),
|
||||
error = function(e) {NULL} )
|
||||
|
||||
if (is.null(tx.json)) {
|
||||
# stop()
|
||||
cat(paste0("tx: ", i, " block: ", height, "\n"), file = "~/RingCT-problems.txt", append = TRUE)
|
||||
next
|
||||
}
|
||||
|
||||
output.amounts <- sapply(tx.json$vout, FUN = function(x) {x$amount})
|
||||
|
||||
tx_size_bytes <- ifelse(i == 1,
|
||||
nchar(rcp.ret$txs[[i]]$pruned_as_hex) / 2,
|
||||
nchar(rcp.ret$txs[[i]]$as_hex) / 2)
|
||||
# Coinbase has special structure
|
||||
# Reference:
|
||||
# https://libera.monerologs.net/monero-dev/20221231
|
||||
# https://github.com/monero-project/monero/pull/8691
|
||||
# https://github.com/monero-project/monero/issues/8311
|
||||
|
||||
calc.tx.weight.clawback <- function(p, is.bpp) {
|
||||
pow.of.two <- 2^(1:4)
|
||||
pow.of.two.index <- findInterval(p, pow.of.two, left.open = TRUE) + 1
|
||||
|
||||
n_padded_outputs <- pow.of.two[pow.of.two.index]
|
||||
|
||||
if (is.bpp) {
|
||||
multiplier <- 6
|
||||
} else {
|
||||
multiplier <- 9
|
||||
}
|
||||
|
||||
bp_base <- (32 * (multiplier + 7 * 2)) / 2
|
||||
nlr <- ceiling(log2(64 * p))
|
||||
bp_size <- 32 * (multiplier + 2 * nlr)
|
||||
transaction_clawback <- (bp_base * n_padded_outputs - bp_size) * 4 / 5
|
||||
floor(transaction_clawback) # With bpp, this is sometimes (always?) not an integer
|
||||
}
|
||||
# Equation from page 63 of Zero to Monero 2.0
|
||||
# Updated with Bulletproofs+
|
||||
# https://github.com/monero-project/monero/blame/c8214782fb2a769c57382a999eaf099691c836e7/src/cryptonote_basic/cryptonote_format_utils.cpp#L106
|
||||
|
||||
|
||||
if (length(tx.json$vout) == 2 || i == 1) {
|
||||
# i == 1 means the first tx, which is the coinbase tx
|
||||
tx_weight_bytes <- tx_size_bytes
|
||||
} else {
|
||||
tx_weight_bytes <- tx_size_bytes +
|
||||
calc.tx.weight.clawback(length(tx.json$vout), length(tx.json$rctsig_prunable$bpp) > 0)
|
||||
}
|
||||
|
||||
|
||||
tx_fee <- ifelse(i == 1 || is.null(tx.json$rct_signatures), NA, tx.json$rct_signatures$txnFee)
|
||||
# missing non-RingCT tx fee
|
||||
|
||||
is.mordinal <-
|
||||
height >= 2838965 &&
|
||||
length(tx.json$vout) == 2 &&
|
||||
i > 1 && # not the first tx, which is the coinbase tx
|
||||
length(tx.json$extra) > 44 &&
|
||||
tx.json$extra[45] == 16
|
||||
# With "&&", evaluates each expression sequentially until it is false (if ever). Then stops.
|
||||
# If all are TRUE, then returns true.
|
||||
|
||||
is.mordinal.transfer <-
|
||||
height >= 2838965 &&
|
||||
length(tx.json$vout) == 2 &&
|
||||
i > 1 && # not the first tx, which is the coinbase tx
|
||||
length(tx.json$extra) > 44 &&
|
||||
tx.json$extra[45] == 17
|
||||
|
||||
output.index.collected[[i]] <- data.table(
|
||||
block_height = height,
|
||||
block_timestamp = block.data$block_header$timestamp,
|
||||
block_size = block.data$block_size,
|
||||
block_reward = block.data$reward,
|
||||
tx_num = i,
|
||||
tx_hash = txs.to.collect[i],
|
||||
tx_version = tx.json$version,
|
||||
tx_fee = tx_fee,
|
||||
tx_size_bytes = tx_size_bytes,
|
||||
tx_weight_bytes = tx_weight_bytes,
|
||||
number_of_inputs = length(tx.json$vin),
|
||||
number_of_outputs = length(tx.json$vout),
|
||||
output_num = seq_along(rcp.ret$txs[[i]]$output_indices),
|
||||
output_index = rcp.ret$txs[[i]]$output_indices,
|
||||
output_amount = output.amounts,
|
||||
output_unlock_time = tx.json$unlock_time,
|
||||
is_mordinal = is.mordinal,
|
||||
is_mordinal_transfer = is.mordinal.transfer)
|
||||
|
||||
|
||||
if (i == 1L) { next }
|
||||
# Skip first tx since it is the coinbase and has no inputs
|
||||
|
||||
tx_hash <- txs.to.collect[i]
|
||||
|
||||
rings <- vector("list", length(tx.json$vin))
|
||||
|
||||
for (j in seq_along(tx.json$vin)) {
|
||||
rings[[j]] <- data.table(
|
||||
tx_hash = tx_hash,
|
||||
input_num = j,
|
||||
input_amount = tx.json$vin[[j]]$key$amount,
|
||||
key_offset_num = seq_along(tx.json$vin[[j]]$key$key_offsets),
|
||||
key_offsets = tx.json$vin[[j]]$key$key_offsets
|
||||
)
|
||||
}
|
||||
|
||||
rings.collected[[i-1]] <- rbindlist(rings)
|
||||
|
||||
}
|
||||
|
||||
output.index.collected <- data.table::rbindlist(output.index.collected)
|
||||
rings.collected <- rbindlist(rings.collected)
|
||||
|
||||
return.data[[height.iter]] <- list(
|
||||
output.index.collected = output.index.collected,
|
||||
rings.collected = rings.collected)
|
||||
|
||||
}
|
||||
|
||||
return.data
|
||||
|
||||
} )
|
||||
})
|
||||
|
||||
future::plan(future::sequential)
|
||||
# Stop thread workers to free RAM
|
||||
|
||||
returned.temp <- vector("list", length(returned))
|
||||
|
||||
for (i in seq_along(returned)) {
|
||||
returned.temp[[i]] <- list(
|
||||
output.index.collected = rbindlist(lapply(returned[[i]],
|
||||
FUN = function(y) { y$output.index.collected })),
|
||||
rings.collected = rbindlist(lapply(returned[[i]],
|
||||
FUN = function(y) { y$rings.collected }))
|
||||
)
|
||||
}
|
||||
|
||||
returned.temp <- list(
|
||||
output.index.collected = rbindlist(lapply(returned.temp,
|
||||
FUN = function(y) { y$output.index.collected })),
|
||||
rings.collected = rbindlist(lapply(returned.temp,
|
||||
FUN = function(y) { y$rings.collected }))
|
||||
)
|
||||
|
||||
output.index <- returned.temp$output.index.collected
|
||||
returned.temp$output.index.collected <- NULL
|
||||
rm(returned.temp)
|
||||
|
||||
output.index[, output_amount_for_index := ifelse(tx_num == 1, 0, output_amount)]
|
||||
|
||||
output.index <- output.index[ !(tx_num == 1 & tx_version == 1), ]
|
||||
# Remove coinbase outputs that are ineligible for use in a RingCT ring
|
||||
# See https://libera.monerologs.net/monero-dev/20230323#c224570
|
||||
|
||||
|
||||
|
||||
output.index.date <- unique(output.index[, .(block_timestamp = block_timestamp)])
|
||||
|
||||
output.index.date[, block_date := as.Date(as.POSIXct(block_timestamp, origin = "1970-01-01"))]
|
||||
|
||||
output.index <- merge(output.index, output.index.date)
|
||||
# speed improvement by splitting and then merging
|
||||
|
||||
gc()
|
||||
|
||||
|
||||
|
||||
BIN
Monero-Black-Marble-Flood/pdf/cost-effectiveness-animation.gif
Normal file
BIN
Monero-Black-Marble-Flood/pdf/cost-effectiveness-animation.gif
Normal file
Binary file not shown.
|
After 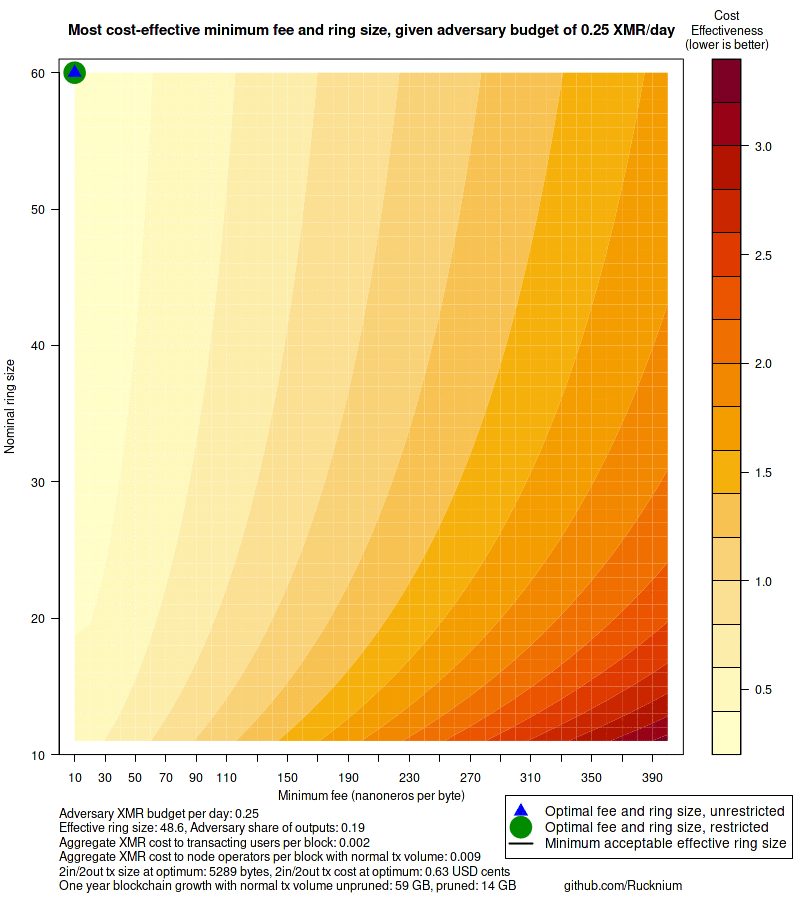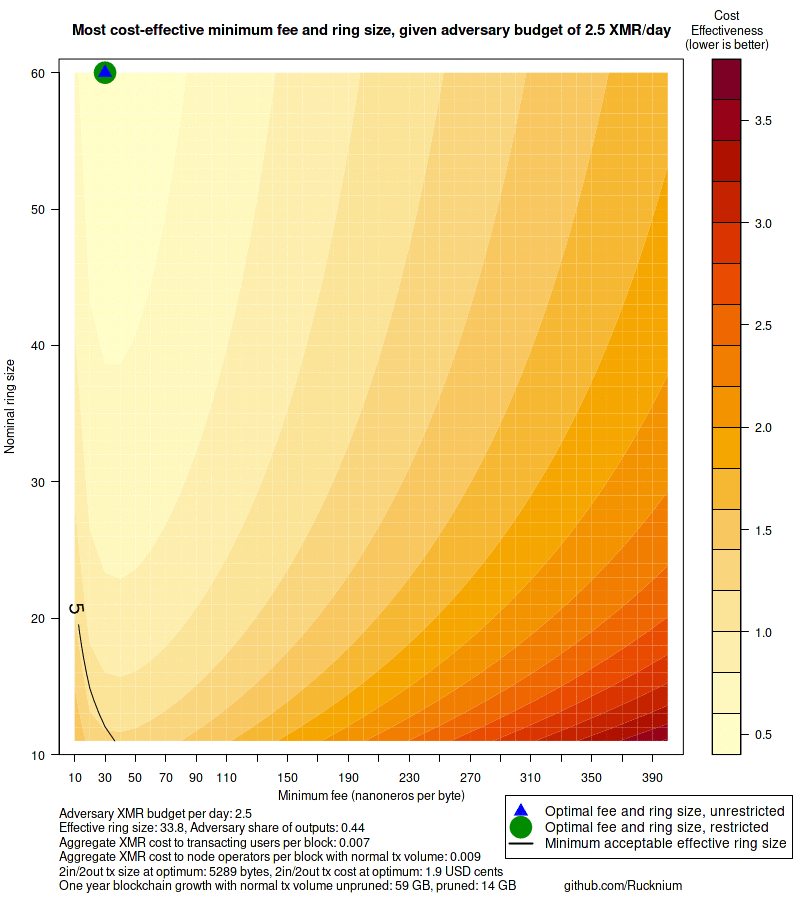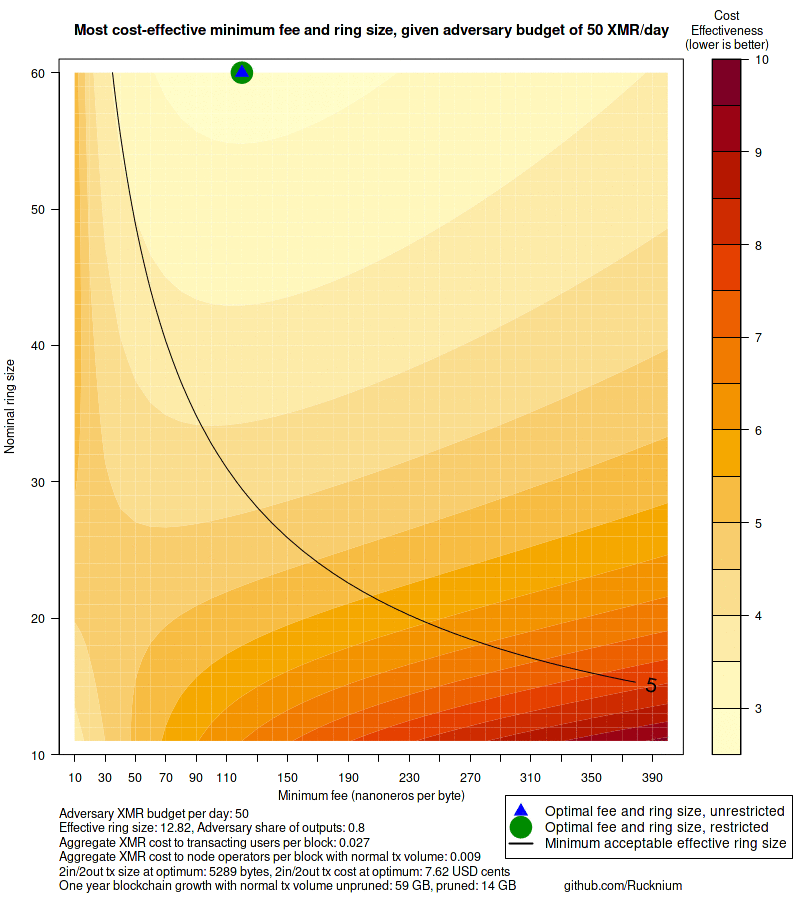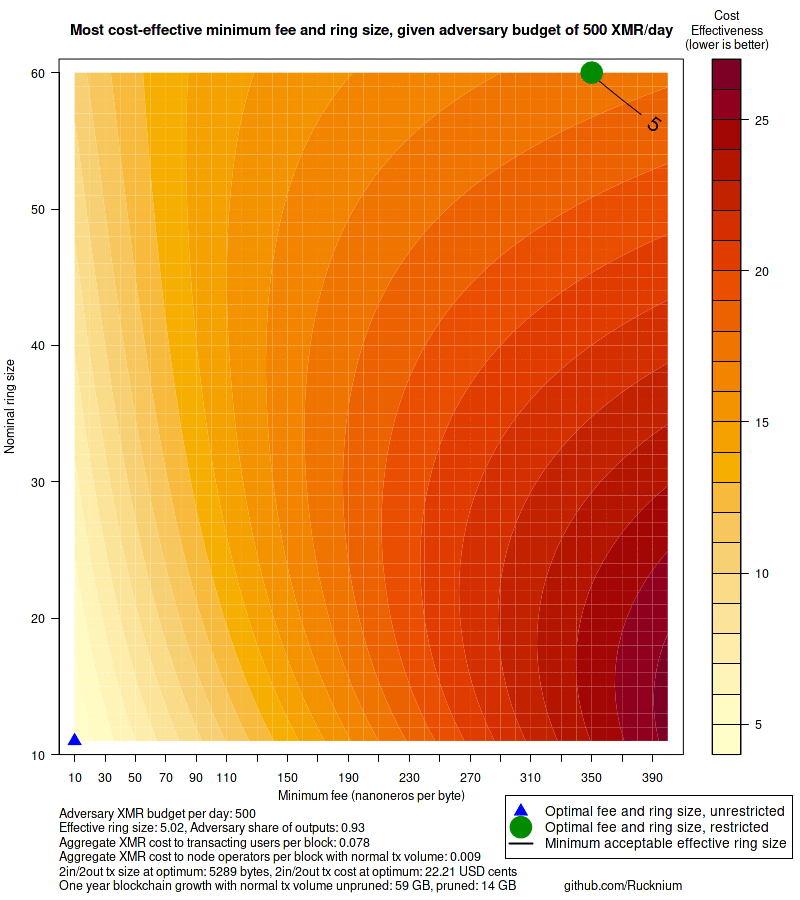
(image error) Size: 1.3 MiB |
Binary file not shown.
|
After 
(image error) Size: 64 KiB |
Binary file not shown.
|
After 
(image error) Size: 18 KiB |
Binary file not shown.
|
After 
(image error) Size: 19 KiB |
Binary file not shown.
|
|
@ -0,0 +1,807 @@
|
|||
|
||||
\documentclass[english]{article}
|
||||
\usepackage[T1]{fontenc}
|
||||
\usepackage[latin9]{inputenc}
|
||||
\usepackage{float}
|
||||
\usepackage{url}
|
||||
\usepackage{amsmath}
|
||||
\usepackage{amssymb}
|
||||
\usepackage{stackrel}
|
||||
\usepackage{graphicx}
|
||||
|
||||
\makeatletter
|
||||
|
||||
|
||||
\usepackage[dvipsnames,table]{xcolor}
|
||||
|
||||
\usepackage{lineno}
|
||||
\linenumbers
|
||||
\linespread{1.25}
|
||||
|
||||
\usepackage{longtable}
|
||||
\usepackage{pdflscape}
|
||||
|
||||
\usepackage[bookmarks=true]{hyperref}
|
||||
\usepackage{orcidlink}
|
||||
\usepackage{booktabs}
|
||||
\usepackage{caption}
|
||||
\usepackage{longtable}
|
||||
% \usepackage[T1]{fontenc}
|
||||
\usepackage{geometry}
|
||||
\geometry{verbose,tmargin=2cm,bmargin=2cm,lmargin=2cm,rmargin=2cm}
|
||||
\usepackage{array}
|
||||
\usepackage{url}
|
||||
\usepackage{multirow}
|
||||
\usepackage{stackrel}
|
||||
\usepackage{rotating}
|
||||
|
||||
\usepackage{bbold}
|
||||
|
||||
|
||||
\usepackage{array} % for ExtraRowHeight
|
||||
|
||||
\usepackage{graphicx}
|
||||
\usepackage{siunitx}
|
||||
\usepackage[normalem]{ulem}
|
||||
\usepackage{colortbl}
|
||||
|
||||
\usepackage{hhline}
|
||||
\usepackage{calc}
|
||||
\usepackage{tabularx}
|
||||
\usepackage{threeparttable}
|
||||
\usepackage{wrapfig}
|
||||
\usepackage{adjustbox}
|
||||
|
||||
|
||||
\usepackage{hyperref}
|
||||
|
||||
\newcolumntype{L}{>{\raggedright\arraybackslash}}
|
||||
\newcolumntype{R}{>{\raggedleft\arraybackslash}}
|
||||
\newcolumntype{C}{>{\centering\arraybackslash}}
|
||||
|
||||
% \renewcommand{\arraystretch}{1.5}
|
||||
\renewcommand{\tabcolsep}{0.2cm}
|
||||
|
||||
\setlength{\LTpre}{6pt}
|
||||
\setlength{\LTpost}{6pt}
|
||||
|
||||
\makeatother
|
||||
|
||||
\usepackage{babel}
|
||||
|
||||
|
||||
|
||||
|
||||
|
||||
% https://tex.stackexchange.com/questions/151241/remove-metadata-of-pdf-generated-by-latex
|
||||
\hypersetup{
|
||||
bookmarks=true, % show bookmarks bar?
|
||||
unicode=false, % non-Latin characters in Acrobat's bookmarks
|
||||
pdftoolbar=true, % show Acrobat's toolbar?
|
||||
pdfmenubar=true, % show Acrobat's menu?
|
||||
pdffitwindow=false, % window fit to page when opened
|
||||
% pdfstartview={FitW}, % fits the width of the page to the window
|
||||
pdftitle={Defeating a Black Marble Flood Against Monero: Best Options for Ring Size and Transaction Fee}, % title
|
||||
pdfauthor={Rucknium}, % author
|
||||
pdfsubject={}, % subject of the document
|
||||
pdfcreator={Rucknium}, % creator of the document
|
||||
pdfproducer={}, % producer of the document
|
||||
pdfkeywords={}, % list of keywords
|
||||
pdfnewwindow=true, % links in new window
|
||||
colorlinks=false, % false: boxed links; true: colored links
|
||||
linkcolor=red, % color of internal links
|
||||
citecolor=green, % color of links to bibliography
|
||||
filecolor=magenta, % color of file links
|
||||
urlcolor=cyan % color of external links
|
||||
}
|
||||
|
||||
|
||||
|
||||
|
||||
\begin{document}
|
||||
|
||||
\title{Defeating a Black Marble Flood Against Monero: Best Options for Ring Size and Transaction Fee\\\vspace{.3cm}
|
||||
\large Draft v0.1\vspace{-.715cm}}
|
||||
\author{Rucknium\orcidlink{0000-0001-5999-8950} }
|
||||
\date{May 28, 2024}
|
||||
|
||||
|
||||
|
||||
|
||||
\maketitle
|
||||
|
||||
\section{Summary}
|
||||
|
||||
Increasing Monero's ring size and minimum transaction fee are two
|
||||
options for defeating black marble flooding. This document attempts
|
||||
to answer the question: Is it better to increase the ring size or
|
||||
the transaction fee, or some combination of the two? Cost-Effectiveness
|
||||
Analysis is used to analyze this question. It considers the additional
|
||||
costs imposed on transacting users and node operators compared to
|
||||
the benefit of stronger resistance to black marble flooding.
|
||||
|
||||
Consider an adversary with a daily budget of 12.5 XMR, five times
|
||||
higher than the daily expenditure of the suspected March 2024 black
|
||||
marble flooder. Given the constraints considered, the most cost-effective
|
||||
combination of defense parameters are ring size 60 and minimum 70
|
||||
nanonero per byte fee. Effective ring size would be 22.8 if the adversary
|
||||
spent his entire budget every day. The 2in/2out reference transaction
|
||||
with ring size 60 would be about 140\% larger than the transaction
|
||||
with current ring size 16. The user's cost to send this transaction
|
||||
would be about 4.4 USD cents. The total time to verify all transactions
|
||||
in a block of normal transaction volume would increase from 0.5 seconds
|
||||
to 1.8 seconds. An unpruned node would grow 59 GB in a year instead
|
||||
of 25 GB. Pruned nodes would grow 14 GB instead of 8 GB.
|
||||
|
||||
\section{Black marble flooding as a game}
|
||||
|
||||
We will analyze the problem as a game with two players. One player
|
||||
aims to flood the Monero blockchain with black marble outputs. This
|
||||
player is limited by his budget. The other player aims to deter the
|
||||
first player, or at least limit the damage, by choosing minimum fee
|
||||
and ring size. This player is limited by the costs that fees and ring
|
||||
size impose of transacting users and node operators.
|
||||
|
||||
Sam is a privacy adversary. His goal is to reduce Monero's effective
|
||||
ring size by flooding the Monero blockchain with black marble outputs
|
||||
that he owns. He has some budget $b$ denominated in XMR to spend
|
||||
on transaction fees per block.
|
||||
|
||||
Alice wishes to defeat Sam. She can set Monero's ring size and minimum
|
||||
transaction fee to try to accomplish her goal. Sam would have to spend
|
||||
more XMR per output if the minimum fee per byte were higher. A larger
|
||||
ring size would require Sam to own a larger share of outputs to achieve
|
||||
a specified effective ring size. (Without changing the minimum fee
|
||||
per byte, a larger ring size also requires Sam to spent more XMR to
|
||||
produce each output because transaction size is larger.)
|
||||
|
||||
Larger ring sizes and fees help Alice accomplish her goal of defeating
|
||||
Sam, but Alice cannot raise ring size and fee without limit. Users
|
||||
who send Monero transactions need to pay a higher fee when the minimum
|
||||
transaction fee is higher. Larger ring sizes mean that transactions
|
||||
are larger. At a given transaction volume, larger transactions make
|
||||
the blockchain grow faster. People who operate Monero nodes need to
|
||||
store the blockchain on their storage media such as Solid State Drives
|
||||
(SSDs). Alice needs to balance the benefit of greater defense against
|
||||
Sam against the cost imposed on transacting users and node operators.
|
||||
|
||||
These are the factors on Alice's mind:
|
||||
\begin{itemize}
|
||||
\item I do not know Sam's budget $b$. I do not know what effective ring
|
||||
size he hopes to achieve. If I set ring size and fee so that he cannot
|
||||
achieve his desired effective ring size with his budget $b$, he will
|
||||
choose not to flood the blockchain with black marbles. This is the
|
||||
deterrence outcome.
|
||||
\item If I fail to deter Sam, at least I can hold him to a specific effective
|
||||
ring size when he spends his budget $b$. This is the fallback outcome.
|
||||
\item I do not want to set ring size and transaction fee unnecessarily high
|
||||
because transacting users and node operators pay higher costs when
|
||||
these parameters increase.
|
||||
\end{itemize}
|
||||
We will simplify the problem:
|
||||
\begin{itemize}
|
||||
\item Sam may actually change the budget he is willing to spend based on
|
||||
the effective ring size he is able to achieve. In other words, Sam
|
||||
may have a tradeoff function between budget and effective ring size.
|
||||
We will ignore this complication and assume that Sam's budget is fixed,
|
||||
but unknown to Alice.
|
||||
\item We will use the fallback outcome to measure the effectiveness of Alice's
|
||||
options. When the fallback outcome is better for Alice, the deterrence
|
||||
outcome is more likely. Therefore, it is a little redundant to compute
|
||||
the probability of the deterrence outcome as an effectiveness metric.
|
||||
\item Transaction volume by normal users is assumed to be constant and unaffected
|
||||
by changes in the transaction fee. In other words, we will assume
|
||||
that the demand for Monero transactions is completely inelastic with
|
||||
respect to transaction fee.
|
||||
\item We will assume that Sam's black marble transactions are 1in/2out because
|
||||
the suspected black marble flood of March 2024 used this type of transaction.
|
||||
Sam could produce black marble outputs more cheaply with 1in/16out
|
||||
transactions, but the flood transactions would be easier for an observer
|
||||
to identify.
|
||||
\end{itemize}
|
||||
Alice will use Cost-Effectiveness Analysis (CEA) to evaluate her ring
|
||||
size and fee options. Cost effectiveness is the ratio of cost to effectiveness:
|
||||
|
||||
\begin{equation}
|
||||
CE=\dfrac{\mathrm{Cost}}{\mathrm{Effectiveness}}
|
||||
\end{equation}
|
||||
|
||||
A lower value of $CE$ is better. Alice must define cost and effectiveness
|
||||
as functions of ring size, transaction fee, and the adversary's budget.
|
||||
Let $n$ be nominal ring size, $f$ be the fee per byte in nanonero
|
||||
units, and $b$ be the adversary's budget. Costs will be measured
|
||||
in terms of XMR per block.
|
||||
|
||||
The cost has two components: cost to transacting users and cost to
|
||||
node operators. The $i$th transaction has some number of inputs and
|
||||
outputs. Changing the ring size $n$ changes the total size of the
|
||||
$i$th transaction, which affects the total minimum fee to send the
|
||||
transactions. And changing the minimum fee per byte changes the total
|
||||
fee, of course. Let $w_{i}\left(n\right)$ be the weight of transaction
|
||||
$i$ when ring size is $n$. When a transaction has two outputs, transaction
|
||||
weight is equal to transaction size in bytes. Weight is larger than
|
||||
size when the number of outputs is greater than two.\footnote{See Section 7.3.2 of koe, Alonso, K. M., \& Noether, S. (2020). \textit{Zero
|
||||
to Monero: Second Edition}.} The block is assumed to contain an average set of transactions $T$.
|
||||
The average is based on observed transactions confirmed on the blockchain
|
||||
in the four weeks before the March 2024 suspected black marble flooding:
|
||||
February 5 -- March 3. $C_{u}\left(f,n\right)$ is the aggregate
|
||||
users' cost to send transactions for an average block:
|
||||
|
||||
\begin{equation}
|
||||
C_{u}\left(f,n\right)=\underset{i\in T}{\sum}f\cdot w_{i}\left(n\right)
|
||||
\end{equation}
|
||||
|
||||
The cost to node operators is a function of ring size. Node operators
|
||||
do not pay higher costs when the minimum transaction fee is higher.
|
||||
All units of computer storage in this document will be SI units, i.e.
|
||||
a kilobyte, megabyte, gigabyte and terabyte are $10^{3}$, $10^{6}$,
|
||||
$10^{9}$, and $10^{12}$ bytes, respectively. The retail price of
|
||||
one consumer 1 TB SATA SSD is about 1 XMR.\footnote{In April 2024, the median retail price of a 1TB SATA SSD on \url{https://ssd.userbenchmark.com/}
|
||||
was 114.50 USD. The exchange rate at the time was 120 USD per XMR.} A node operator's cost $C_{SSD}$ to store one byte of Monero blockchain
|
||||
data is $10^{-12}$ XMR (a piconero). According to \texttt{monero.fail/map},
|
||||
there were about 20,000 Monero nodes on the network in April 2024.
|
||||
Currently the minimum relay fee is 20,000 piconeros (20 nanoneros)
|
||||
per byte. Therefore, by coincidence Monero transactions pay for their
|
||||
own storage space on the node network when users pay the minimum fee
|
||||
per byte.
|
||||
|
||||
Let $d_{n}$, the number of nodes (daemons), be 20,000. $z_{i}\left(n\right)$
|
||||
is the size of the $i$th transaction in the $T$ set when ring size
|
||||
is $n$. The $m$ is an adjustment parameter that raises or lowers
|
||||
total node operators' costs by a linear factor to adjust for uncertainty
|
||||
about the true number of nodes and to add costs that are more difficult
|
||||
to compute like CPU and RAM use. In the analysis below $m$ will be
|
||||
set to 2. We will assume that each node is an unpruned node that stores
|
||||
all transaction data in full. The total cost to node operators is
|
||||
the sum of the size of transactions in the $T$ set multiplied by
|
||||
the storage cost on a single SSD, the number of nodes on the network,
|
||||
and the $m$ adjustment parameter:
|
||||
|
||||
\begin{equation}
|
||||
C_{d}\left(n,m\right)=m\cdot d_{n}\cdot C_{SSD}\cdot\underset{i\in T}{\sum}z_{i}\left(n\right)
|
||||
\end{equation}
|
||||
|
||||
Notice that $C_{d}\left(n,m\right)$ is the cost to node operators
|
||||
under normal transaction volume, i.e. when there is no black marble
|
||||
flooding. Total cost is the sum of $C_{u}\left(f,n\right)$ and $C_{d}\left(n,m\right)$:
|
||||
|
||||
\begin{equation}
|
||||
C\left(f,n,m\right)=C_{u}\left(f,n\right)+C_{d}\left(n,m\right)
|
||||
\end{equation}
|
||||
|
||||
With budget $b$, Sam can afford to place $\frac{b}{f}$ bytes of
|
||||
transaction data in a block. Sam would create transactions with one
|
||||
input and two outputs. The formula for the number of bytes of a transaction
|
||||
like this in terms of the ring size $n$ is $975+35n$. The $975$
|
||||
bytes is the size of the transaction except for the linear cost of
|
||||
the ring size, i.e. a (invalid) 1in/2out transaction with ring size
|
||||
0 would have $975$ bytes composed of the input's key image, other
|
||||
input data that does not scale up with ring size, the outputs' bulletproofs+,
|
||||
the outputs' public key, and \texttt{tx\_extra} data. The $35$ coefficient
|
||||
on $n$ is the sum of the bytes of the ``$s$'' component of the
|
||||
CLSAG ring signature of each ring member (32 bytes) and $3$ bytes
|
||||
of the key offset integer that is used to create the output indices
|
||||
of the ring members. The $3$ bytes is an empirical average of the
|
||||
byes used by each key offset integer. The number of outputs per byte
|
||||
that Sam produces is $2/\left(975+35n\right)$ because each of his
|
||||
transaction has two outputs. To calculate the number of outputs per
|
||||
block that Sam can afford with budget $b$ when fee is $f$ and nominal
|
||||
ring size is $n$, we compute the product of $\frac{b}{f}$ and $2/\left(975+35n\right)$,
|
||||
producing the formula for $s\left(b,f,n\right)$:
|
||||
|
||||
\begin{equation}
|
||||
s\left(b,f,n\right)=\dfrac{2b}{f\cdot\left(975+35n\right)}
|
||||
\end{equation}
|
||||
|
||||
Let $r$ be the number of real user outputs. When the number of outputs
|
||||
owned by Sam is $s\left(b,f,n\right)$, the long-term mean effective
|
||||
ring size\footnote{For a derivation of mean effective ring size, see Section 3 of Draft
|
||||
v0.2 of Rucknium (2024) ``March 2024 Suspected Black Marble Flooding
|
||||
Against Monero: Privacy, User Experience, and Countermeasures'' \url{https://github.com/Rucknium/misc-research/blob/main/Monero-Black-Marble-Flood/pdf/monero-black-marble-flood.pdf}} is
|
||||
|
||||
\begin{equation}
|
||||
n_{e}\left(b,f,n\right)=1+\left(n-1\right)\cdot\dfrac{r}{r+s\left(b,f,n\right)}\label{eq:expectation-n_e}
|
||||
\end{equation}
|
||||
|
||||
Alice wants to have a larger $n_{e}$ when Sam is producing black
|
||||
marbles. $n_{e}$ is the desired outcome in the cost-effectiveness
|
||||
analysis:
|
||||
|
||||
\begin{equation}
|
||||
CE=\dfrac{C\left(f,n,m\right)}{n_{e}\left(b,f,n\right)}\label{eq:cost-effectiveness-full}
|
||||
\end{equation}
|
||||
|
||||
Alice's goal is to choose minimum fee per byte $f$ and nominal ring
|
||||
size $n$ to minimize $CE$ when Sam spends his budget $b$ producing
|
||||
black marbles and the node cost multiplier is some specified $m$.
|
||||
In game theory, a player's \textit{best response} in a two-player
|
||||
game is a strategy that gives the player the best payoff when the
|
||||
other player plays some specified strategy. Alice's best response
|
||||
to Sam playing some $b$ as a strategy is to set $f$ and $n$ to
|
||||
minimize $CE$. Alice does not know what value of $b$ Sam intends
|
||||
to play, but reasonable values of $b$ can be analyzed to guide reasonable
|
||||
choices of $f$ and $n$. In game theory terms, Alice's uncertainty
|
||||
about Sam's $b$ means that this is a game of imperfect information.
|
||||
Sam's player ``type'' is the unknown $b$. Sam has some probability
|
||||
of being each type. In this document I will not explicitly declare
|
||||
some probability distribution of Sam's type, but one could determine
|
||||
Alice's single best response for the expected value of her cost effectiveness
|
||||
when Sam's type has some probability distribution.
|
||||
|
||||
Define $f_{\min}$ and $f_{\max}$ as the minimum and maximum $f$
|
||||
that Alice is willing to set. Let $n_{\min}$ and $n_{\max}$ be the
|
||||
minimum and maximum $n$ that Alice is willing to set. Assume that
|
||||
Alice wants to make sure that the effective ring size does not fall
|
||||
below some specified minimum acceptable limit $\check{n}_{e}$. Alice
|
||||
will try to minimize (\ref{eq:cost-effectiveness-full}) except when
|
||||
the effective ring size would be below $\check{n}_{e}$ at the minimum
|
||||
of (\ref{eq:cost-effectiveness-full}). In that case, Alice will exclude
|
||||
the values of $n$ and $f$ that cause effective ring size to be below
|
||||
$\check{n}_{e}$, then choose $n$ and $f$ to minimize (\ref{eq:cost-effectiveness-full})
|
||||
from the set of $n$ and $f$ values that remain.
|
||||
|
||||
Alice's best response correspondence given Sam's choice of $b$ and
|
||||
the node cost multiplier $m$ is the solution to
|
||||
|
||||
\begin{equation}
|
||||
\begin{array}{l}
|
||||
\underset{f,n}{\arg\min}\dfrac{C\left(f,n,m\right)}{n_{e}\left(b,f,n\right)}\\
|
||||
\mathrm{subject\,to}\\
|
||||
f_{\min}\leq f,\,f\leq f_{\max}\\
|
||||
n_{\min}\leq n,\,n\leq n_{\max}\\
|
||||
\check{n}_{e}\leq n_{e}\left(b,f,n\right)
|
||||
\end{array}\label{eq:best-response-correspondence}
|
||||
\end{equation}
|
||||
|
||||
The problem in (\ref{eq:best-response-correspondence}) is a nonlinear
|
||||
minimization problem with nonlinear inequality constraints. Note that
|
||||
the constraint set is convex, but the objective function is neither
|
||||
globally convex nor globally concave.\footnote{The full proof of this statement is TODO. The first four constraints
|
||||
form a convex set because they are affine. The $\check{n}_{e}\leq n_{e}\left(b,f,n\right)$
|
||||
constraint is more complicated. The Hessian matrix of the second-order
|
||||
partial derivatives of $n_{e}$ with respect to $f$ and $n$ is negative
|
||||
definite as long as $n>1$. That means that its superlevel set for
|
||||
some $\check{n}_{e}$ is convex. (The $\check{n}_{e}\leq n_{e}\left(b,f,n\right)$
|
||||
inequality defines the superlevel set.) The intersection of two convex
|
||||
sets is convex, so the constraint set of (\ref{eq:best-response-correspondence})
|
||||
is convex.} The necessary conditions for the solution could be found analytically
|
||||
by checking the Karush-Kuhn-Tucker conditions. I will solve it numerically
|
||||
with a grid search. The grid is formed by evaluating (\ref{eq:cost-effectiveness-full})
|
||||
many times at different values of $f$ and $n$. The values of $f$
|
||||
are 40 equally-spaced values between $f_{\min}$ and $f_{\max}$.
|
||||
The values of $n$ are each integer between $n_{\min}$ and $n_{\max}$.
|
||||
|
||||
We will start with a simple example. Assume that the adversary's budget
|
||||
is 2.5 XMR per day. This is approximately the expenditure rate of
|
||||
the suspected black marble flooder in March 2024. We will evaluate
|
||||
cost-effectiveness at each combination of $f=\left\{ 10,20,40,100,200\right\} $
|
||||
nanoneros per byte and $n=\left\{ 16,30,45,60\right\} $ ring size.
|
||||
|
||||
Table \ref{table-2_5-budget} contains the cost effectiveness (CE)
|
||||
computations with other metrics like transaction size, total projected
|
||||
growth of the blockchain, and estimated transaction verification time.
|
||||
Note that the cost to send a 2in/2out transaction increases when ring
|
||||
size increases even if the fee per byte does not increase because
|
||||
users have to pay for larger total transaction size. The numerator
|
||||
of CE has been scaled to millineros. The lowest value in the CE column
|
||||
is 0.48 when nominal ring size is 60 and minimum fee is 40 nanoneros
|
||||
per byte. Sam can achieve a 37.5 effective ring size with a 2.5 XMR/day
|
||||
budget when nominal ring size is 60 and minimum fee is 40 nanoneros
|
||||
per byte. Estimation of transaction and block verification time is
|
||||
explained in Appendix \ref{sec:Appendix:-Transaction-verification}..
|
||||
|
||||
Figure \ref{fig-contour-plot-50-budget} is a shaded contour plot
|
||||
of cost effectiveness when Sam has a budget of 50 XMR per day. Lighter
|
||||
colors on the plot indicate lower CE values at the specified minimum
|
||||
fee and ring size values. The blue triangle indicates the fee and
|
||||
ring size values that minimize the CE when the minimum acceptable
|
||||
effective ring size of 5 is disregarded. When we allow only fee and
|
||||
ring size values that produce effective ring size above the minimum
|
||||
acceptable effective ring, the green circle indicates the fee and
|
||||
ring size values that minimize the CE. In this plot the triangle and
|
||||
circle are at the same location because the minimum CE produces an
|
||||
effective ring size of 12.8, above the minimum effective ring size
|
||||
of 5.
|
||||
|
||||
Table \ref{table-scenarios-budget} shows the values of minimum fee
|
||||
and ring size that produce optimal cost effectiveness when Sam has
|
||||
different budgets. The maximum budget, 500 XMR per day, exceeds Monero's
|
||||
daily security budget provided by tail emission. An adversary's budget
|
||||
higher than 500 might imply that the adversary could directly 51 percent
|
||||
attack the blockchain by renting CPU hashpower. It seems unnecessary
|
||||
to consider a black marble flooder's budget greater than 500 XMR per
|
||||
day because an adversary with a higher budget might be able to do
|
||||
more damage to Monero than flooding the blockchain with black marble
|
||||
outputs.
|
||||
|
||||
\begin{landscape}
|
||||
\footnotesize{
|
||||
\input{tables/permuted-cost-effectiveness-2_5-budget.tex}
|
||||
}
|
||||
\end{landscape}
|
||||
|
||||
\begin{figure}
|
||||
\caption{Most cost-effective minimum fee and ring size when adversary budget
|
||||
is 50 XMR per day}
|
||||
|
||||
\label{fig-contour-plot-50-budget}
|
||||
|
||||
\includegraphics[scale=0.65]{images/cost-effective-contour-plot-50-budget}
|
||||
\end{figure}
|
||||
|
||||
\begin{landscape}
|
||||
\footnotesize{
|
||||
\input{tables/cost-effectiveness-budget-scenarios.tex}
|
||||
}
|
||||
\end{landscape}
|
||||
|
||||
\section{Discussion}
|
||||
|
||||
What have we learned? According to this analysis, raising the ring
|
||||
size is a more cost-effective strategy against a black marble
|
||||
attack than raising fees. A combination of a large increase in ring
|
||||
size and a modest increase in fee seems to provide a good, cost-effective
|
||||
defense.
|
||||
|
||||
Consider an adversary with a daily budget of 12.5 XMR, five times
|
||||
higher than the daily expenditure of the suspected March 2024 black
|
||||
marble flooder. Table \ref{table-scenarios-budget} says the most
|
||||
cost-effective combination of defense parameters are ring size 60
|
||||
and minimum 70 nanonero per byte fee. Effective ring size would be
|
||||
22.8 if Sam spent his entire budget every day. The 2in/2out reference
|
||||
transaction with ring size 60 would be about 140\% larger than the
|
||||
transaction with current ring size 16. The user's cost to send this
|
||||
transaction would be about 4.4 USD cents. The total time to verify
|
||||
all transactions in a block of normal transaction volume would increase
|
||||
from 0.5 seconds to 1.8 seconds. An unpruned node would grow 59 GB
|
||||
in a year instead of 25 GB. Pruned nodes would grow 14 GB instead
|
||||
of 8 GB.
|
||||
|
||||
Put these storage requirements into perspective. Recall that we use
|
||||
base-10 (SI) units to measure bytes in this document. As of May 2024,
|
||||
a unpruned Monero blockchain is 206 GB. A pruned Monero node takes
|
||||
79 GB of storage space. The 2023 Ultra 4K edition of Call of Duty
|
||||
requires 229 GB of storage.\footnote{{\scriptsize{}\url{https://web.archive.org/web/20231214215231/https://www.callofduty.com/blog/2023/10/call-of-duty-modern-warfare-III-specs-preloading-pc-trailer}}}
|
||||
An unpruned BTC node requires 650 GB of storage and grows about 89
|
||||
GB per year.\footnote{\url{https://bitcoin.stackexchange.com/a/116350} and \url{https://transactionfee.info/charts/block-size/}}
|
||||
Therefore, with ring size 60 the Monero blockchain would grow slower
|
||||
than the BTC blockchain, crossing the Call of Duty storage threshold
|
||||
within a year.
|
||||
|
||||
Encouraging node operators to prune their nodes and implementing a
|
||||
coinbase consolidation transaction type could reduce the impact of
|
||||
increasing the minimum fee and ring size. Pruning could be encouraged
|
||||
by setting pruning as the default in more Monero software interfaces,
|
||||
such as the Monero GUI wallet Pull Request \#4320, and public information
|
||||
campaigns.\footnote{\url{https://github.com/monero-project/monero-gui/pull/4320}}
|
||||
A coinbase consolidation type would reduce the transaction size for
|
||||
small coinbase outputs.\footnote{\url{https://github.com/monero-project/research-lab/issues/108}}
|
||||
|
||||
\section{Summary: Downsides and benefits of options}
|
||||
\begin{enumerate}
|
||||
\item Increase the minimum relay fee per byte
|
||||
\begin{enumerate}
|
||||
\item Downsides:
|
||||
\begin{enumerate}
|
||||
\item Users may make fewer transactions. That would reduce Monero's total
|
||||
anonymity set because the rate of creation of new outputs would fall.
|
||||
\item Users could move to another means of payment.
|
||||
\item Monero might lose its reputation as a low-cost means of payment.
|
||||
\item Large changes in Monero's fiat exchange rate could make the purchasing
|
||||
power of the minimum fee much higher or lower than anticipated.
|
||||
\end{enumerate}
|
||||
\item Benefits:
|
||||
\begin{enumerate}
|
||||
\item Miners would earn more from fees. This would increase Monero's resistance
|
||||
to 51 percent attack because its mining security budget would increase
|
||||
a little.
|
||||
\item Higher fees would increase the cost of all spam regardless of motivation.
|
||||
(Increasing the ring size only negatively affects spammers that want
|
||||
to reduce the effective ring size.)
|
||||
\end{enumerate}
|
||||
\end{enumerate}
|
||||
\item Increase the ring size
|
||||
\begin{enumerate}
|
||||
\item Downsides:
|
||||
\begin{enumerate}
|
||||
\item Greater storage requirements for operating a Monero node could cause
|
||||
some node operators to stop running their nodes. This would make the
|
||||
Monero network less decentralized.
|
||||
\item Some Monero wallet users may stop running local nodes and switch to
|
||||
remote nodes. This would increase the load on public remote nodes
|
||||
and potentially expose the wallet users to some privacy risks from
|
||||
malicious remote nodes.\footnote{See \url{https://docs.featherwallet.org/guides/nodes}}
|
||||
\item Verification time per transaction would increase. During normal operation,
|
||||
the Monero node would use more CPU resources. During initial blockchain
|
||||
download, total sync time would be greater. Syncing a Monero node
|
||||
on a HDD, which is already very difficult, might become completely
|
||||
nonviable because of the necessary random reads for ring signature
|
||||
verification.
|
||||
\item At extremes, long verification times can threaten network stability.
|
||||
In 2023 Pirate Chain suffered a transaction spam attack that caused
|
||||
chain splits because of long transaction verification times.\footnote{\url{https://web.archive.org/web/20230803171107/https://old.reddit.com/user/SignificantRoof5656/comments/15h9reh/pirate_chains_045_spam_attack_2_months_later/}}
|
||||
Monero uses the Fluffy Blocks protocol to verify transactions as they
|
||||
arrive in the txpool instead of bottlenecking verification at the
|
||||
time new blocks are mined. It is unclear if Pirate Chain, a code fork
|
||||
of Zcash, uses a compact block protocol.\footnote{See \url{https://github.com/zcash/zips/issues/360}}
|
||||
As long as the time to verify each block's transactions does not become
|
||||
a large fraction of mean time between blocks (120 seconds), this is
|
||||
probably not a threatening issue, \textit{in theory}. In practice,
|
||||
the Monero node performs many more actions than just verifying the
|
||||
cryptography of transactions. There may be hidden bottlenecks. Recently,
|
||||
spikes of transactions with large numbers of inputs have seemed to
|
||||
cause excess RAM usage of nodes, shutting down nodes in some cases.\footnote{\url{https://github.com/monero-project/monero/issues/9317}}
|
||||
\end{enumerate}
|
||||
\item Benefits:
|
||||
\begin{enumerate}
|
||||
\item Increasing the ring size increases the anonymity set of all transaction
|
||||
inputs. Other statistical attacks unrelated to black marble flooding
|
||||
like EAE attacks and timing analysis would become more difficult.
|
||||
\end{enumerate}
|
||||
\item Neutral:
|
||||
\begin{enumerate}
|
||||
\item Increasing the ring size has very little effect on wallet sync times.
|
||||
The bandwidth costs for syncing transactions in mined blocks are only
|
||||
about three bytes per ring member for the ring offset data. No additional
|
||||
computation is required. However, ring signature data is sent from
|
||||
nodes to wallets when transactions are still in the txpool.\footnote{Thanks to jeffro256 for explaining this.}
|
||||
\end{enumerate}
|
||||
\end{enumerate}
|
||||
\item Encourage blockchain pruning
|
||||
\begin{enumerate}
|
||||
\item Downsides:
|
||||
\begin{enumerate}
|
||||
\item New unpruned nodes may have to connect to more nodes to create an
|
||||
unpruned copy of the blockchain.
|
||||
\item All pruned nodes keep one-eighth of the transaction data that is designated
|
||||
``prunable''. If all nodes on the network are pruned, there is an
|
||||
extremely small chance that one of the eight pruning slices will not
|
||||
exist on the whole network. That would mean that not all signature
|
||||
data on the blockchain could be verified. When blockchain pruning
|
||||
is enabled, a Monero node randomly chooses one of eight possible pruning
|
||||
seeds independently of the pruning seeds that other nodes have chosen.
|
||||
By chance, the network could be missing one of the eight slices of
|
||||
the pruneable part of the blockchain because the choice of pruning
|
||||
seed is not coordinated between nodes. This chance is extremely small.
|
||||
If the network only has pruned nodes and the total number of nodes
|
||||
on the network is 681, the probability of missing one of the eight
|
||||
pruning slices is less than $2^{-128}$, which is the probability
|
||||
of guessing a specific 12-word BIP39 bitcoin seed phrase with a single
|
||||
guess. See Appendix \ref{sec:Probability-of-recovering-complete-blockchain-data}
|
||||
for how to compute this probability. This probability does not consider
|
||||
the challenge of new nodes finding their pruning slices by connecting
|
||||
to multiple nodes throughout the network.
|
||||
\end{enumerate}
|
||||
\item Benefits:
|
||||
\begin{enumerate}
|
||||
\item Pruned nodes consume much less storage space.
|
||||
\end{enumerate}
|
||||
\item Neutral:
|
||||
\begin{enumerate}
|
||||
\item ``There are no privacy or security downsides when using a pruned
|
||||
node.''\footnote{\url{https://web.getmonero.org/resources/moneropedia/pruning.html}}
|
||||
\end{enumerate}
|
||||
\end{enumerate}
|
||||
\item Implement ``Coinbase Consolidation Tx Type''\footnote{\url{https://github.com/monero-project/research-lab/issues/108}}
|
||||
\begin{enumerate}
|
||||
\item Downsides:
|
||||
\begin{enumerate}
|
||||
\item koe, the original proper of this protocol modification, said, ``After
|
||||
thinking more, I am not sure this proposal is the right direction.
|
||||
Enote consolidation being statistically significant, and consolidating
|
||||
enotes with small amounts being expensive, is a general problem not
|
||||
specific to coinbase enotes. Implementing a specific solution for
|
||||
coinbase enotes amounts to elevating the circumstances of miners to
|
||||
first-class status in the protocol, without solving the more general
|
||||
problem. If another major project on the scale of p2pool becomes active
|
||||
in Monero and would benefit from specific protocol changes (not trivial
|
||||
benefits - privacy and scaling benefits even), should we hard fork
|
||||
to accommodate them? To support protocol longevity by reducing hardforks
|
||||
(and not setting precedents that would justify a relatively higher
|
||||
rate of future hardforks), it seems better to aim for general solutions
|
||||
to problems. In this case, one general solution to the privacy impacts
|
||||
of consolidation would be a global membership proof. The cost of consolidations
|
||||
might be addressed by using aggregate membership proofs that scale
|
||||
sub-linearly with the number of memberships being proven (i.e. number
|
||||
of tx inputs).''\footnote{\url{https://github.com/monero-project/research-lab/issues/108\#issuecomment-1379288635}}
|
||||
\item There is a small privacy impact to some miners. Most centralized mining
|
||||
pools already publish the blocks that they mine, so the ownership
|
||||
of mining pools' coinbases is usually publicly known already.\footnote{Wijaya, D. A., Liu, J. K., Steinfeld, R., \& Liu, D. (2021) ``Transparency
|
||||
or anonymity leak: Monero mining pools data publication''. Paper
|
||||
presented at Information Security and Privacy - 26th Australasian
|
||||
Conference, ACISP 2021, Virtual Event, December 1-3, 2021, Proceedings.} P2Pool payout addresses are public on the P2Pool side chain, allowing
|
||||
good guesses about which transactions are consolidating coinbases
|
||||
to specific mining addresses.\footnote{\url{https://p2pool.observer/sweeps}}
|
||||
The P2Pool README recommends miners to use a separate mining wallet.\footnote{\url{https://github.com/SChernykh/p2pool?tab=readme-ov-file\#general-considerations}}
|
||||
Therefore, a coinbase consolidation transaction type would not have
|
||||
a large negative impact on the privacy of most miners because the
|
||||
on-chain privacy for miners is low to begin with. The privacy of solo
|
||||
miners could be negatively impacted, however. With the new transaction
|
||||
consolidation type, those miners could send coins to themselves once
|
||||
to create outputs that would enter the non-coinbase anonymity set.
|
||||
\end{enumerate}
|
||||
\item Benefits:
|
||||
\begin{enumerate}
|
||||
\item If the coinbase consolidation transaction type is implemented at the
|
||||
same time as much larger rings, coinbase consolidations would not
|
||||
take up so much storage. In the 60 ring member scenario, annual blockchain
|
||||
growth would be 2.7 GB less if all coinbase outputs are spent by inputs
|
||||
with ring size one.
|
||||
\item If the ring size and/or fee per byte increases a lot, P2Pool mining
|
||||
may become uncompetitive compared to centralized pool mining, especially
|
||||
for the P2Pool mini chain. Consider the 10th percentile of multi-output
|
||||
coinbase outputs during February 2024: 0.000272 XMR. (10\% of the
|
||||
likely P2Pool outputs are below this amount.) With the status quo
|
||||
ring size and minimum fee per byte, consolidating this P2Pool payout
|
||||
by adding an input to a transaction costs the miner about 5 percent
|
||||
of the value of that output. With the ring size 60 and 70 nanoneros
|
||||
per byte scenario considered above, about 57 percent of the value
|
||||
of that output would be consumed by the cost to spent the output in
|
||||
a transaction's output. But if coinbase outputs only have to have
|
||||
ring size 1, then even paying 60 nanoneros per byte would cost the
|
||||
miner only 4.2 percent of the output's value when you spent it in
|
||||
a 1-ring-member input. (The cost quoted here do not include the bytes
|
||||
contributed by outputs or other transaction data.)
|
||||
\item Coinbase outputs can behave like black marbles in the rings of transactions
|
||||
that do not spend coinbase outputs. See the ``Avoiding selecting
|
||||
coinbase outputs as decoys'' Monero Research Lab issue.\footnote{\url{https://github.com/monero-project/research-lab/issues/109}}
|
||||
Implementing a coinbase consolidation transaction type would prevent
|
||||
coinbase outputs from being included in the rings of transactions
|
||||
that do not spend coinbase outputs. This would improve the privacy
|
||||
of those transactions.
|
||||
\end{enumerate}
|
||||
\end{enumerate}
|
||||
\end{enumerate}
|
||||
|
||||
\appendix
|
||||
\newpage{}
|
||||
|
||||
\section{Appendix: Transaction verification time estimates\label{sec:Appendix:-Transaction-verification}}
|
||||
|
||||
The verification time estimates are based on performance tests developed
|
||||
by koe. I modified the test parameters to produce estimates of a large
|
||||
set of ring sizes, input counts, and output counts in \url{https://github.com/Rucknium/monero-tx-performance}.
|
||||
koe provides interpretation of the performance tests in Monero Research
|
||||
Lab issue $\#91$.\footnote{\url{https://github.com/monero-project/research-lab/issues/91}}
|
||||
I used the same machine as koe for the tests. The verification performance
|
||||
tests do not include the time to read data from storage media. The
|
||||
2in/2out reference transaction and the assumed 1in/2out black marble
|
||||
transaction type could be tested directly, but there were too many
|
||||
permutations of the real transaction in/out types in the February-March
|
||||
2024 sample to test those directly. Estimates of the real transaction
|
||||
verification type were necessary to estimate the verification time
|
||||
for an average real block. All tests were in batches of one because
|
||||
setting the batching parameter did not seem to affect the verification
|
||||
time of inputs (it did affect verification time of outputs, but the
|
||||
research question is about varying different ring sizes of inputs,
|
||||
not outputs).
|
||||
|
||||
A linear regression model was fit by Ordinary Least Squares (OLS)
|
||||
to interpolate the estimated verification times for the set of real
|
||||
transactions at different ring sizes. The performance test developed
|
||||
by koe were originally designed to only compute ring sizes that are
|
||||
powers of two. Therefore, ring size performance was tested for ring
|
||||
size 1, 2, 4, 8, 16, 32, and 64. The number of outputs tested was
|
||||
every integer between 2 and 16 because these are the allowed number
|
||||
of transaction outputs by blockchain consensus rules. The maximum
|
||||
number of inputs in a single transaction that a standard Monero wallet
|
||||
can produce is 150. The number of inputs I used for the performance
|
||||
estimates was:
|
||||
|
||||
$\{1,2,3,4,5,6,7,8,9,10,20,30,40,50,60,70,80,90,100,110,120,130,140,150\}$
|
||||
|
||||
Taking all permutations of these sets gives $7\cdot15\cdot24=2520$
|
||||
permutations. Tests with these permutations produce the dataset used
|
||||
in the OLS regression. We can guess a good functional form for the
|
||||
regression equation based on knowledge of the time complexity of the
|
||||
algorithms used to cryptographically verify transaction components.
|
||||
I included ring size and inputs, the base 2 log of each, and their
|
||||
interaction terms. Dummy variables of the ceiling of base-2 log of
|
||||
the number of outputs was included in the regression equation since
|
||||
bulletproofs verification times is a function of the integer ceiling
|
||||
of the power of two of the number of outputs in the transaction. The
|
||||
full regression equation is below.
|
||||
|
||||
\begin{equation}
|
||||
\begin{array}{cl}
|
||||
time= & \beta_{0}+\beta_{1}ring\_size+\beta_{2}inputs+\beta_{3}\log_{2}(ring\_size)+\beta_{4}\log_{2}(inputs)+\beta_{5}\mathbb{{1}}\left\{ \lceil\log_{2}(outputs)\rceil=2\right\} \\
|
||||
& +\beta_{6}\mathbb{{1}}\left\{ \lceil\log_{2}(outputs)\rceil=3\right\} +\beta_{7}\mathbb{{1}}\left\{ \lceil\log_{2}(outputs)\rceil=4\right\} \\
|
||||
& +\beta_{8}ring\_size\times inputs+\beta_{9}\log_{2}(ring\_size)\times\log_{2}(inputs)+\epsilon
|
||||
\end{array}\label{eq:verification-time-regression}
|
||||
\end{equation}
|
||||
|
||||
$\lceil x\rceil$ means the integer ceiling of $x$. $\mathbb{{1}}\left\{ x\right\} $
|
||||
is an indicator function. Its value is $1$ when the statement in
|
||||
braces is true and is $0$ otherwise. The results of the regression
|
||||
are in Table \ref{table-regression-results}.. The adjusted $R^{2}$
|
||||
is extremely high (0.9998), indicating that the model fits the data
|
||||
well. However, a model may have a high $R^{2}$ when the scale of
|
||||
the different observations is vastly different, which is the case
|
||||
here.
|
||||
|
||||
Given the estimated parameters from (\ref{eq:verification-time-regression}),
|
||||
predicted values of the verification time for all types of transactions
|
||||
and all ring sizes can be computed for the February-March 2024 sample
|
||||
by plugging the number of inputs, outputs, and ring size into the
|
||||
regression equation with the $\hat{\boldsymbol{\beta}}$ estimated
|
||||
parameters.
|
||||
|
||||
\begin{table}[H]
|
||||
\caption{CLSAG transaction verification time OLS regression. Units are milliseconds.}
|
||||
|
||||
\input{tables/verification-time-regression.tex}
|
||||
|
||||
\label{table-regression-results}
|
||||
\end{table}
|
||||
|
||||
\newpage{}
|
||||
|
||||
\section{Probability of recovering complete blockchain data from a network
|
||||
with only pruned nodes\label{sec:Probability-of-recovering-complete-blockchain-data}}
|
||||
|
||||
The problem of collecting all eight of the Monero's pruning slices
|
||||
is a type of coupon collector's problem. Holst (1986) provides the
|
||||
formula to find the probability that you need $n$ pruned nodes on
|
||||
the network to be able to recover the intact blockchain from the eight
|
||||
unique slices.\footnote{Holst, L. (1986). ``On Birthday, Collectors\textquoteright , Occupancy
|
||||
and Other Classical Urn Problems.'' International Statistical Review
|
||||
/ Revue Internationale de Statistique, 54(1), 15--27. https://doi.org/10.2307/1403255} Holst says, ``In this paper we will consider problems connected
|
||||
with drawing with replacement from an urn with $r$ balls of different
|
||||
colours.....The inverse of the occupancy problem is sometimes called
|
||||
the coupon collector's problem. It reads: how many draws are necessary
|
||||
for obtaining $k$ different balls?'' Holst gives the general problem
|
||||
when $r$ is not necessarily equal to $k$. In the pruned node problem,
|
||||
we only need one copy of each unique slice, so $r=k$ in our case.
|
||||
Holst says that the probability of needing exactly $n$ draws for
|
||||
obtaining $k$ different balls when the urn has $r$ balls of different
|
||||
colors is
|
||||
|
||||
\begin{equation}
|
||||
\mathrm{P}\left(W_{k:r}=n\right)=r_{(k)}S(n-1,k-1)/r^{n}\label{eq:coupon-collectors}
|
||||
\end{equation}
|
||||
|
||||
Holst defines $r_{(k)}\equiv r(r-1)\ldots(r-k+1)$. When $r=k$, this
|
||||
is the factorial $r_{(k)}=r!$. $S(n,k)$ is a Stirling number of
|
||||
the second kind:
|
||||
|
||||
\[
|
||||
S(n,k)=\stackrel[j=0]{k}{\sum}(-1)^{j}\dbinom{k}{j}(k-j)^{n}
|
||||
\]
|
||||
|
||||
The (\ref{eq:coupon-collectors}) equation is the probability that
|
||||
you need exactly $n$ nodes on the network to have all eight distinct
|
||||
slices. We want to know the probability that you need more than $n$
|
||||
nodes to have all the slices. This probability is $1-\sum_{i=8}^{n}\mathrm{P}\left(W_{k:r}=i\right)$.
|
||||
|
||||
To avoid limitations of floating point computer arithmetic, when computing
|
||||
these values it is recommended to use a software library that uses
|
||||
arbitrary-precision numbers such as the GNU Multiple Precision Arithmetic
|
||||
Library.
|
||||
|
||||
Figure \ref{fig-pruned-node-collectors-problem} plots the probability
|
||||
that a Monero network would not contain all 8 pruned node slices.
|
||||
When there are 100 nodes on the network, the probability is about
|
||||
0.001 percent. When the number of nodes is 681, the probability of
|
||||
not having all 8 pruned node slices is less than $2^{-128}$, which
|
||||
is the probability of guessing a specific 12-word BIP39 bitcoin seed
|
||||
phrase with a single guess.\footnote{\url{https://github.com/bitcoin/bips/blob/master/bip-0039.mediawiki}}
|
||||
These probabilities correspond to a network in a single point in time.
|
||||
If we consider that a network will have many ``draws'' in its lifetime,
|
||||
then the probability of missing one of the eight slices during any
|
||||
point in its lifetime is higher. If the whole set of $n$ nodes re-draws
|
||||
its random pruning seed $q$ times, the probability of never missing
|
||||
one of the eight slices is $\left(1-\mathrm{P}\left(\mathrm{missing\,at\,least\,one\,slice}\right)\right)^{q}$
|
||||
because the draws are independent.
|
||||
|
||||
\begin{figure}
|
||||
|
||||
\caption{Probability of not having all 8 distinct pruned slices on the Monero
|
||||
network}
|
||||
|
||||
\label{fig-pruned-node-collectors-problem}
|
||||
|
||||
\includegraphics[scale=0.4]{images/pruned-node-collectors-problem-to-100}\includegraphics[scale=0.4]{images/pruned-node-collectors-problem-to-1000}
|
||||
|
||||
\end{figure}
|
||||
|
||||
\end{document}
|
||||
2522
Monero-Black-Marble-Flood/pdf/performance-test/CLSAG-performance.txt
Normal file
2522
Monero-Black-Marble-Flood/pdf/performance-test/CLSAG-performance.txt
Normal file
File diff suppressed because it is too large
Load diff
|
|
@ -0,0 +1,30 @@
|
|||
\setlength{\LTpost}{0mm}
|
||||
\begin{longtable}{Rp{1.75cm}Rp{1cm}Rp{1.5cm}Rp{0.75cm}Rp{1cm}Rp{2cm}Rp{1.5cm}Rp{0.75cm}Rp{1.4cm}Rp{1cm}Rp{1cm}Rp{1cm}Rp{1cm}Rp{1cm}Rp{0.75cm}Rp{1.4cm}}
|
||||
\caption{
|
||||
{\large Minimum fee and ring size at optimal cost effectiveness, adversary budget scenarios}
|
||||
} \\
|
||||
\toprule
|
||||
& & & & & & & \multicolumn{4}{c}{Normal tx volume} & \multicolumn{5}{c}{Normal tx volume + black marble flooding} \\
|
||||
\cmidrule(lr){8-11} \cmidrule(lr){12-16}
|
||||
& & & & & & & & & \multicolumn{4}{c}{One year blockchain growth (GB)} & & & \\
|
||||
\cmidrule(lr){10-13}
|
||||
Adversary XMR budget per day & Nominal ring size & Min fee (nanoneros per byte) & CE & Size of 2in/2out (bytes) & User's cost to send 2in/2out (USD cents) & Seconds to verify 2in/2out & Block size (KB) & Seconds to verify txs in block & Unpruned & Pruned & Unpruned & Pruned & Effective ring size & Block size (KB) & Seconds to verify txs in block \\
|
||||
\midrule\addlinespace[2.5pt]
|
||||
\cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$2.50$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{16}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$20$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$1.08$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$2,219$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$0.53$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$0.012$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$95$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$0.54$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$25$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$8$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$71$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$21$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$5.41$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$269$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$1.62$}} \\
|
||||
$0.25$ & 60 & $10$ & $0.24$ & $5,289$ & $0.63$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $68$ & $17$ & $48.60$ & $258$ & $2.18$ \\
|
||||
$0.50$ & 60 & $10$ & $0.29$ & $5,289$ & $0.63$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $77$ & $19$ & $40.89$ & $293$ & $2.53$ \\
|
||||
$1.25$ & 60 & $20$ & $0.37$ & $5,289$ & $1.27$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $82$ & $20$ & $37.90$ & $310$ & $2.71$ \\
|
||||
$2.50$ & 60 & $30$ & $0.48$ & $5,289$ & $1.90$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $89$ & $22$ & $33.80$ & $339$ & $3.01$ \\
|
||||
$5.00$ & 60 & $40$ & $0.66$ & $5,289$ & $2.54$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $104$ & $26$ & $27.84$ & $397$ & $3.60$ \\
|
||||
$12.50$ & 60 & $70$ & $1.10$ & $5,289$ & $4.44$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $124$ & $30$ & $22.76$ & $471$ & $4.37$ \\
|
||||
$25.00$ & 60 & $90$ & $1.73$ & $5,289$ & $5.71$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $160$ & $39$ & $17.11$ & $609$ & $5.78$ \\
|
||||
$50.00$ & 60 & $120$ & $2.83$ & $5,289$ & $7.62$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $211$ & $52$ & $12.82$ & $802$ & $7.77$ \\
|
||||
$125.00$ & 60 & $140$ & $5.68$ & $5,289$ & $8.89$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $385$ & $94$ & $7.17$ & $1,464$ & $14.56$ \\
|
||||
$250.00$ & 60 & $180$ & $9.69$ & $5,289$ & $11.42$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $566$ & $138$ & $5.12$ & $2,152$ & $21.64$ \\
|
||||
$500.00$ & 60 & $350$ & $17.47$ & $5,289$ & $22.21$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $580$ & $142$ & $5.02$ & $2,208$ & $22.20$ \\
|
||||
\bottomrule
|
||||
\label{table-scenarios-budget}
|
||||
\end{longtable}
|
||||
\begin{minipage}{\linewidth}
|
||||
Row in green is the status quo\\
|
||||
\end{minipage}
|
||||
|
|
@ -0,0 +1,38 @@
|
|||
\setlength{\LTpost}{0mm}
|
||||
\begin{longtable}{Rp{1.75cm}Rp{1cm}Rp{1.5cm}Rp{0.75cm}Rp{1cm}Rp{2cm}Rp{1.5cm}Rp{0.75cm}Rp{1.4cm}Rp{1cm}Rp{1cm}Rp{1cm}Rp{1cm}Rp{1cm}Rp{0.75cm}Rp{1.4cm}}
|
||||
\caption{
|
||||
{\large Cost effectiveness of minimum fee and ring size options when adversary budget is 2.5 XMR per day}
|
||||
} \\
|
||||
\toprule
|
||||
& & & & & & & \multicolumn{4}{c}{Normal tx volume} & \multicolumn{5}{c}{Normal tx volume + black marble flooding} \\
|
||||
\cmidrule(lr){8-11} \cmidrule(lr){12-16}
|
||||
& & & & & & & & & \multicolumn{4}{c}{One year blockchain growth (GB)} & & & \\
|
||||
\cmidrule(lr){10-13}
|
||||
Adversary XMR budget per day & Nominal ring size & Min fee (nanoneros per byte) & CE & Size of 2in/2out (bytes) & User's cost to send 2in/2out (USD cents) & Seconds to verify 2in/2out & Block size (KB) & Seconds to verify txs in block & Unpruned & Pruned & Unpruned & Pruned & Effective ring size & Block size (KB) & Seconds to verify txs in block \\
|
||||
\midrule\addlinespace[2.5pt]
|
||||
$2.50$ & 16 & $10$ & $1.36$ & $2,219$ & $0.27$ & $0.012$ & $95$ & $0.54$ & $25$ & $8$ & $116$ & $34$ & $3.59$ & $443$ & $2.69$ \\
|
||||
\cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$2.50$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{16}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$20$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$1.08$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$2,219$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$0.53$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$0.012$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$95$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$0.54$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$25$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$8$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$71$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$21$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$5.41$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$269$}} & \cellcolor[HTML]{00FF00}{\textcolor[HTML]{000000}{$1.62$}} \\
|
||||
$2.50$ & 16 & $40$ & $0.99$ & $2,219$ & $1.07$ & $0.012$ & $95$ & $0.54$ & $25$ & $8$ & $48$ & $14$ & $7.82$ & $182$ & $1.08$ \\
|
||||
$2.50$ & 16 & $100$ & $1.21$ & $2,219$ & $2.66$ & $0.012$ & $95$ & $0.54$ & $25$ & $8$ & $34$ & $10$ & $11.14$ & $130$ & $0.75$ \\
|
||||
$2.50$ & 16 & $200$ & $1.75$ & $2,219$ & $5.33$ & $0.012$ & $95$ & $0.54$ & $25$ & $8$ & $30$ & $9$ & $13.10$ & $113$ & $0.64$ \\
|
||||
$2.50$ & 30 & $10$ & $0.97$ & $3,196$ & $0.38$ & $0.022$ & $136$ & $0.94$ & $36$ & $10$ & $127$ & $34$ & $7.25$ & $483$ & $3.82$ \\
|
||||
$2.50$ & 30 & $20$ & $0.74$ & $3,196$ & $0.77$ & $0.022$ & $136$ & $0.94$ & $36$ & $10$ & $81$ & $22$ & $11.29$ & $310$ & $2.38$ \\
|
||||
$2.50$ & 30 & $40$ & $0.69$ & $3,196$ & $1.53$ & $0.022$ & $136$ & $0.94$ & $36$ & $10$ & $59$ & $16$ & $16.19$ & $223$ & $1.66$ \\
|
||||
$2.50$ & 30 & $100$ & $0.87$ & $3,196$ & $3.83$ & $0.022$ & $136$ & $0.94$ & $36$ & $10$ & $45$ & $12$ & $22.26$ & $171$ & $1.23$ \\
|
||||
$2.50$ & 30 & $200$ & $1.29$ & $3,196$ & $7.67$ & $0.022$ & $136$ & $0.94$ & $36$ & $10$ & $40$ & $11$ & $25.54$ & $153$ & $1.09$ \\
|
||||
$2.50$ & 45 & $10$ & $0.76$ & $4,242$ & $0.51$ & $0.032$ & $180$ & $1.38$ & $47$ & $12$ & $138$ & $35$ & $12.31$ & $527$ & $4.68$ \\
|
||||
$2.50$ & 45 & $20$ & $0.59$ & $4,242$ & $1.02$ & $0.032$ & $180$ & $1.38$ & $47$ & $12$ & $93$ & $24$ & $19.00$ & $353$ & $3.03$ \\
|
||||
$2.50$ & 45 & $40$ & $0.56$ & $4,242$ & $2.04$ & $0.032$ & $180$ & $1.38$ & $47$ & $12$ & $70$ & $18$ & $26.55$ & $267$ & $2.21$ \\
|
||||
$2.50$ & 45 & $100$ & $0.73$ & $4,242$ & $5.09$ & $0.032$ & $180$ & $1.38$ & $47$ & $12$ & $56$ & $15$ & $35.14$ & $215$ & $1.71$ \\
|
||||
$2.50$ & 45 & $200$ & $1.10$ & $4,242$ & $10.18$ & $0.032$ & $180$ & $1.38$ & $47$ & $12$ & $52$ & $13$ & $39.45$ & $197$ & $1.55$ \\
|
||||
$2.50$ & 60 & $10$ & $0.63$ & $5,289$ & $0.63$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $150$ & $37$ & $18.37$ & $571$ & $5.39$ \\
|
||||
$2.50$ & 60 & $20$ & $0.50$ & $5,289$ & $1.27$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $104$ & $26$ & $27.84$ & $397$ & $3.60$ \\
|
||||
\cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$2.50$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{60}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$40$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$0.48$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$5,289$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$2.54$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$0.043$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$223$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$1.82$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$59$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$14$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$82$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$20$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$37.90$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$310$}} & \cellcolor[HTML]{FFA500}{\textcolor[HTML]{000000}{$2.71$}} \\
|
||||
$2.50$ & 60 & $100$ & $0.65$ & $5,289$ & $6.35$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $68$ & $17$ & $48.60$ & $258$ & $2.18$ \\
|
||||
$2.50$ & 60 & $200$ & $1.01$ & $5,289$ & $12.69$ & $0.043$ & $223$ & $1.82$ & $59$ & $14$ & $63$ & $16$ & $53.69$ & $241$ & $2.00$ \\
|
||||
\bottomrule
|
||||
\label{table-2_5-budget}
|
||||
\end{longtable}
|
||||
\begin{minipage}{\linewidth}
|
||||
Row in green is the status quo. Row in orange is the best cost effectiveness.\\
|
||||
\end{minipage}
|
||||
|
|
@ -0,0 +1,108 @@
|
|||
|
||||
\providecommand{\huxb}[2]{\arrayrulecolor[RGB]{#1}\global\arrayrulewidth=#2pt}
|
||||
\providecommand{\huxvb}[2]{\color[RGB]{#1}\vrule width #2pt}
|
||||
\providecommand{\huxtpad}[1]{\rule{0pt}{#1}}
|
||||
\providecommand{\huxbpad}[1]{\rule[-#1]{0pt}{#1}}
|
||||
\begin{tabular}{l l}
|
||||
|
||||
|
||||
\hhline{>{\huxb{0, 0, 0}{0.8}}->{\huxb{0, 0, 0}{0.8}}-}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}c!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\centering \hspace{6pt} \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{c!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\centering \hspace{6pt} (1) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{>{\huxb{255, 255, 255}{0.4}}->{\huxb{0, 0, 0}{0.4}}-}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} (Intercept) \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} -0.555 (0.766) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} ring size \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 0.218 *** (0.015) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} inputs \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} -0.141 *** (0.006) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} $\log_{2}$(ring size) \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 0.670 ** (0.234) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} $\log_{2}$(inputs) \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 3.956 *** (0.181) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} $\lceil\log_{2}(\mathrm{outputs})\rceil = $ 2 \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 3.462 *** (0.558) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} $\lceil\log_{2}(\mathrm{outputs})\rceil = $ 3 \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 9.906 *** (0.510) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} $\lceil\log_{2}(\mathrm{outputs})\rceil = $ 4 \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 21.783 *** (0.484) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} ring size $\times$ inputs \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 0.254 *** (0.000) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} $\log_{2}$(ring size) $\times$ $\log_{2}$(inputs) \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} -1.362 *** (0.044) \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{>{\huxb{255, 255, 255}{0.4}}->{\huxb{0, 0, 0}{0.4}}-}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} N \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 2520\hphantom{0}\hphantom{0}\hphantom{0}\hphantom{0}\hphantom{0} \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{1}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} Adjusted R-squared \hspace{6pt}\huxbpad{6pt}} &
|
||||
\multicolumn{1}{r!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedleft \hspace{6pt} 0.9998 \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{>{\huxb{0, 0, 0}{0.8}}->{\huxb{0, 0, 0}{0.8}}-}
|
||||
\arrayrulecolor{black}
|
||||
|
||||
\multicolumn{2}{!{\huxvb{0, 0, 0}{0}}l!{\huxvb{0, 0, 0}{0}}}{\huxtpad{6pt + 1em}\raggedright \hspace{6pt} Standard errors in parentheses. *** p $<$ 0.001; ** p $<$ 0.01; * p $<$ 0.05. \hspace{6pt}\huxbpad{6pt}} \tabularnewline[-0.5pt]
|
||||
|
||||
|
||||
\hhline{}
|
||||
\arrayrulecolor{black}
|
||||
\end{tabular}
|
||||
Loading…
Reference in a new issue